해당 포스팅은 '밑바닥부터 시작하는 딥러닝2'를 공부하고 정리, 요약한 글입니다. 모든 내용은 해당 도서를 기준으로 합니다.

◼️ 2.1 자연어 처리란
한국어와 영어 등 우리가 평소에 쓰는 말을 자연어라고 한다.
자연어처리(Natural Language Processing, NLP)를 문자 그대로 해석하면 '자연어를 처리하는 분야'이고 우리의 말을 컴퓨터에게 이해시키기 위한 기술이다.
◼️ 2.2 시소러스
시소러스란 유의어 사전으로 '뜻이 같은 단어(동의어)'나 '뜻이 비슷한 단어(유의어)'가 한 그룹으로 분류되어 있다.
자연어 처리에 이용되는 시소러스에서는 단어 사이의 '상위와 하위' 혹은 '전체와 부분' 등 더 세세한 관곆ㅏ지 정의해둔 경우가 있다.
모든 단어에 대한 유의어 집합을 만든 다음 단어들의 관계를 그래프로 표현하여 단어 사이의 연결을 정의할 수 있다. 이 단어 네트워크를 이용하여 컴퓨터에게 단어 사이의 관계를 가르칠 수 있다.
◾ 2.2.1 WordNet
자연어 처리 분야에서 가장 유명한 시소러스는 WordNet이다. WordNet을 사용하면 유의어를 얻거나 '단어 네트워크'를 이용할 수 있다.
◾ 2.2.2 시소러스의 문제점
WordNet과 같은 시소러스에슨 수많은 단어에 대한 동의어와 계층 구조 등의 관계가 정의돼 있다. 이 지식을 이용하면 '단어의 의미'를 컴퓨터에 전달할 수 있다.
시소러스 방식의 대표적인 문제점들은 다음과 같다.
- 시대 변화에 대응하기 어렵다.
- 사람을 쓰는 비용은 크다.
- 단어의 미묘한 차이를 표현할 수 없다.
◼️ 2.3 통계 기반 기법
통계 기반 기법을 살펴보면서 말뭉치(corpus)를 이용할 것이다. 맹목적으로 수집된 텍스트 데이터가 아닌 자연어 처리 연구나 애플리케이션을 염두에 두고 수집된 테스트 데이터를 일반적으로 '말뭉치'라고 한다.
말뭉치에는 자연어에 대한 사람의 '지식'이 충분히 담겨 있다고 볼 수 있다.
◾ 2.3.1 파이썬으로 말뭉치 전처리하기
파이썬에서 텍스트 데이터(말뭉치)에 전처리를 하는 것은 텍스트 데이터를 단어로 분할하고 그 분할된 단어들을 단어 ID 목록으로 변환하는 일이다.
text = 'You say goodbye and I say hello.'
text = text.lower()
text = text.replace('.', ' .')
text
>> 'you say goodbye and i say hello .'
words = text.split(' ')
words
>> ['you', 'say', 'goodbye', 'and', 'i', 'say', 'hello', '.']
단어에 ID를 부여하고 ID의 리스트로 이용할 수 있도록 해준다.
word_to_id = {}
for word in words:
if word not in word_to_id:
new_id = len(word_to_id)
word_to_id[word] = new_id
id_to_word = {id_: word for word, id_ in word_to_id.items()}
id_to_word
>> {0: 'you', 1: 'say', 2: 'goodbye', 3: 'and', 4: 'i', 5: 'hello', 6: '.'}
word_to_id
>> {'you': 0, 'say': 1, 'goodbye': 2, 'and': 3, 'i': 4, 'hello': 5, '.': 6}
# 단어 ID 검색, 단어 ID가지고 단어 검색하기
id_to_word[1]
>> 'say'
word_to_id['hello']
>> 5
import numpy as np
corpus = [word_to_id[word] for word in words]
corpus = np.array(corpus)
corpus
>> array([0, 1, 2, 3, 4, 1, 5, 6])
# common/util.py -> preprocess 메서드 사용
import sys
sys.path.append('..')
from common.util import preprocess
text = 'You say goodbye and I say hello.'
corpus, word_to_id, id_to_word = preprocess(text)
corpus, word_to_id, id_to_word
>> (array([0, 1, 2, 3, 4, 1, 5, 6]),
{'you': 0, 'say': 1, 'goodbye': 2, 'and': 3, 'i': 4, 'hello': 5, '.': 6},
{0: 'you', 1: 'say', 2: 'goodbye', 3: 'and', 4: 'i', 5: 'hello', 6: '.'})
◾ 2.3.2 단어의 분산 표현
우리가 원하는 것은 '단어의 의미'를 정확하게 파악할 수 있는 벡터 표현이다. 이를 자연어 처리 분야에서는 단어의 분산 표현(distributional representation)이라고 한다.
◾ 2.3.3 분포 가설
자연어 처리 연구는 단어의 의미는 주변 단어에 의해 형성된다는 아이디어에 뿌리를 두고 있다. 이를 분포 가설이라고 한다.
분포 가설은 단어 자체에는 의미가 없고 그 단어가 사용된 맥락(context)이 의미를 형성한다는 것이다.
◾ 2.3.4 동시발생 행렬
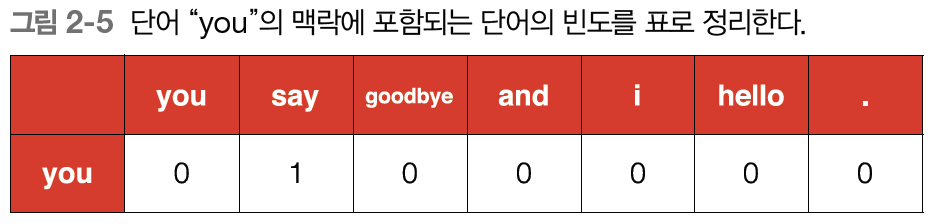
주변 단어를 세는 방법으로 특정 단어에 대해 그 단어의 주변에 어떤 단어가 몇번이나 등장하는지 카운팅하여 합치는 방법이다.
import sys
sys.path.append('..')
import numpy as np
from common.util import preprocess
text = 'You say goodbye and I say hello.'
corpus, word_to_id, id_to_word = preprocess(text)
print(f'corpus: {corpus}')
print(f'id_to_word: {id_to_word}')
>> corpus: [0 1 2 3 4 1 5 6]
id_to_word: {0: 'you', 1: 'say', 2: 'goodbye', 3: 'and', 4: 'i', 5: 'hello', 6: '.'}



# 동시발생행렬을 자동화 하는 함수
def create_co_matrix(corpus, vocab_size, window_size=1):
corpus_size = len(corpus)
co_matrix = np.zeros((vocab_size, vocab_size), dtype=np.int32)
for idx, word_id in enumerate(corpus):
for i in range(1, window_size + 1):
left_idx = idx - i # left window_size
right_idx = idx + i # right window_size
if left_idx >= 0:
left_word_id = corpus[left_idx]
co_matrix[word_id, left_word_id] += 1
if right_idx < corpus_size:
right_word_id = corpus[right_idx]
co_matrix[word_id, right_word_id] += 1
return co_matrix
◾ 2.3.5 벡터 간 유사도
벡터 사이의 유사도를 측정한느 방법은 벡터의 내적이나 유클리드 거리 등이 있다.
단어 벡터의 유사도를 나타낼 때는 코사인 유사도를 자주 이용한다.

노름은 벡터의 크기를 나타낸 것으로 이 식의 핵심은 벡터를 정규화하고 내적을 구하는 것이다.
def cos_similarity(x, y, eps=1e-8):
nx = x / np.sqrt(np.sum(x**2)) # x의 정규화
ny = y / np.sqrt(np.sum(y**2)) # y의 정규화
return np.dot(nx, ny)인수로 제로 벡터가 들어오면 오류가 발생하기 때문에 이를 해결하기 위해 전통적으로 분모에 작은 값을 더해준다.
def cos_similarity(x, y, eps=1e-8):
nx = x / np.sqrt(np.sum(x**2) + eps) # x의 정규화
ny = y / np.sqrt(np.sum(y**2) + eps) # y의 정규화
return np.dot(nx, ny)
◾ 2.3.6 유사 단어의 랭킹 표시
def most_similar(query, word_to_id, id_to_word, word_matrix, top=5):
# 1) 검색어를 꺼낸다.
if query not in word_to_id:
print(f'{query}(을)를 찾을 수 없습니다.')
return
print(f'\n[query] {query}')
query_id = word_to_id[query]
query_vec = word_matrix[query_id]
# 2) 코사인 유사도 계산
vocab_size = len(id_to_word)
similarity = np.zeros(vocab_size)
for i in range(vocab_size):
similarity[i] = cos_similarity(word_matrix[i], query_vec)
# 3) 코사인 유사도를 기준으로 내림차순으로 출력
count = 0
for i in (-1 * similarity).argsort():
if id_to_word[i] == query:
continue
print(f' {id_to_word[i]}: {similarity[i]}')
count +=1
if count >= top:
return
◼️ 2.4 통계 기반 기법 개선하기
◾ 2.4.1 상호정보량
동시발생 행렬의 원소는 두 단어가 동시에 발생한 횟수를 나타낸다. 발생 횟수라는 것은 사실 그리 좋은 특징이 아니다.
두 단어의 동시발생 횟수는 많지만 강한 관련성을 가지지 않을 때가 있는데 이럴 땐 점별 상호정보량(Pointwise Mutual Information, PMI)라는 척도를 사용한다.
PMI는 확률 변수 x와 y에 대해 다음 식으로 정의 된다.

P(x)는 x가 일어날 확률, P(y)는 y가 일어날 확률, P(x,y)는 x와 y가 동시에 일어날 확률을 뜻한다.
동시발생 행렬을 사용해서 식 2.2를 다시 쓰면 다음과 같다.

PMI를 이용하면 단어가 단독으로 출현하는 횟수가 고려 된다.
PMI에도 두 단어의 동시발생 횟수가 0이면 log20이 마이너스 무한이 되어버리는 문제가 있다. 이 문제를 피하기 위해 실제로 구현할 때는 양의 상호정보량(PPMI)를 사용한다.

이 식에 따라 PMI가 음수일 땐 0으로 취급하며 단어 사이의 관련성을 0 이상의 실수로 나타낼 수 있게 된다.
# 동시발생 행렬을 PPMI 행렬로 변환하는 함수
def ppmi(C, verbose=False, eps=1e-8):
'''PPMI(점별 상호정보량) 생성
:param C: 동시발생 행렬
:param verbose: 진행 상황을 출력할지 여부
:return: ppmi
'''
M = np.zeros_like(C, dtype=np.float32)
N = np.sum(C) # num of corpus
S = np.sum(C, axis=0) # 각 단어의 출현 횟수
total = C.shape[0] * C.shape[1]
cnt = 0
for i in range(C.shape[0]):
for j in range(C.shape[1]):
pmi = np.log2(C[i, j] * N / (S[i]*S[j]) + eps)
M[i, j] = max(0, pmi)
if verbose:
cnt += 1
if cnt % (total//100) == 0:
print(f'{(100*cnt/total):.2f} 완료')
return M
PPMI도 말뭉치의 어휘 수가 증가함에 따라 각 단어 벡터의 차원 수도 증가한다는 문제가 있다. 원소 대부분이 0이게 되는데 벡터의 원소 대부분이 중요도가 낮다는 의미인데, 이런 벡터는 노이즈에 약하고 견고하지 못하다는 약점이 있다.
이런 문제에 대처하고자 자주 수행하는 기법이 벡터의 차원 감소 이다.
◾ 2.4.2 차원 감소
차원 감소는 문자 그대로 벡터의 차원을 줄이는 방법을 말한다. 이는 중요한 정보는 최대한 유지하면서 줄이는 게 핵심이다.
아래 그림과 같이 데이터의 분포를 고려해 중요한 '축'을 찾는 일을 수행한다.

왼쪽은 데이터즘들을 2차원 좌표에 표시한 모습이며 오른쪽은 새로운 축을 도입하여 똑같은 데이터를 좌표축 하나만으로 표시한 그림이다.
각 데이터점의 값은 새로운 축으로 사영된 값으로 변한다. 중요한 것은 가장 적합한 축을 찾아내는 일로 1차원 값만으로도 데이터의 본질적인 차이를 구별할 수 있어야 한다는 것이다.
차원을 감소시키는 방법은 특잇값분해(Singular Value Decomposition, SVD)이 있다.
SVD는 임의의 행렬을 세 행렬의 곱으로 분해하며 수식으로는 다음과 같다.

◾ 2.4.3 SVD에 의한 차원 감소
# count_method_small.py
%matplotlib inline
import sys
sys.path.append('..')
import numpy as np
import matplotlib.pyplot as plt
from common.util import preprocess, create_co_matrix, ppmi
text = 'You say goodbye and I say hello.'
corpus, word_to_id, id_to_word = preprocess(text)
vocab_size = len(word_to_id)
C = create_co_matrix(corpus, vocab_size)
W = ppmi(C)
# SVD
U, S, V = np.linalg.svd(W)print(C[0]) # 동시발생 행렬
print(W[0]) # PPMI 행렬
print(U[0]) # SVD
# 2차원으로 차원 축소하기
print(U[0, :2])
>> [0 1 0 0 0 0 0]
[0. 1.807 0. 0. 0. 0. 0. ]
[ 3.409e-01 0.000e+00 -1.205e-01 -3.886e-16 -9.323e-01 -1.110e-16
-2.426e-17]
[0.341 0. ]# 플롯
for word, word_id in word_to_id.items():
plt.annotate(word, (U[word_id, 0], U[word_id, 1]))
plt.scatter(U[:,0], U[:,1], alpha=0.5)
plt.show()
◾ 2.4.4 & 2.4.5 PTB 데이터셋 평가
펜 트리뱅크(Penn Treebank, PTB) 데이터셋의 말뭉치는 주어진 기법의 품질을 측정하는 벤치마크로 자주 이용된다.
import sys
sys.path.append('..')
from dataset import ptb
corpus, word_to_id, id_to_word = ptb.load_data('train')
print('말뭉치 크기:', len(corpus))
print('corpus[:30]:', corpus[:30])
print()
print('id_to_word[0]:', id_to_word[0])
print('id_to_word[1]:', id_to_word[1])
print('id_to_word[2]:', id_to_word[2])
print()
print("word_to_id['car']:", word_to_id['car'])
print("word_to_id['happy']:", word_to_id['happy'])
print("word_to_id['lexus']:", word_to_id['lexus'])
>> 말뭉치 크기: 929589
corpus[:30]: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
24 25 26 27 28 29]
id_to_word[0]: aer
id_to_word[1]: banknote
id_to_word[2]: berlitz
word_to_id['car']: 3856
word_to_id['happy']: 4428
word_to_id['lexus']: 7426
# PTB 데이터셋 평가
import sys
sys.path.append('..')
import numpy as np
from common.util import most_similar, create_co_matrix, ppmi
from dataset import ptb
window_size = 2
wordvec_size = 100
corpus, word_to_id, id_to_word = ptb.load_data('train')
vocab_size = len(word_to_id)
print('Create Co-occurrence Matrix...')
C = create_co_matrix(corpus, vocab_size, window_size)
>> Create Co-occurrence Matrix...print('PPMI 계산...')
W = ppmi(C, verbose=True)
>> PPMI 계산...
1.00 완료
2.00 완료
3.00 완료
4.00 완료
5.00 완료
6.00 완료
7.00 완료
...
95.00 완료
96.00 완료
97.00 완료
98.00 완료
99.00 완료
100.00 완료try:
# truncated SVD
from sklearn.utils.extmath import randomized_svd
U, S, V = randomized_svd(W, n_components=wordvec_size, n_iter=5,
random_state=None)
except:
# SVD
U, S, V = np.linalg.svd(W)
word_vecs = U[:, :wordvec_size]
querys = ['you', 'year', 'car', 'toyota']
for query in querys:
most_similar(query, word_to_id, id_to_word, word_vecs, top=5)
>> [query] you
i: 0.6474241018295288
we: 0.6223806738853455
do: 0.5163971185684204
've: 0.49530309438705444
'll: 0.4937693476676941
[query] year
earlier: 0.6766989827156067
quarter: 0.6463431119918823
next: 0.6242960095405579
month: 0.6221592426300049
last: 0.5859693288803101
[query] car
luxury: 0.661283016204834
auto: 0.6432934403419495
truck: 0.5961803793907166
cars: 0.5737640261650085
corsica: 0.5673944354057312
[query] toyota
motor: 0.7801448106765747
nissan: 0.7088394165039062
motors: 0.691170871257782
honda: 0.6479698419570923
mazda: 0.5932565331459045
◼️ 2.5 정리
- WordNet 등의 시소러스를 이용하면 유의어를 얻거나 단어 사이의 유사도를 측정하는 등 유용한 작업을 할 수 있다.
- 현재는 말뭉치를 이용해 단어를 벡터화하는 방식이 주로 쓰인다.
- 최근의 단어 벡터화 기법들은 대부분 단어의 의미는 주변 단어에 의해 형성된다는 분포 가설에 기초한다.
- 통계 기반 기법은 말뭉치 안의 각 단어에 대해서 그 단어의 주변 단어의 빈도를 집계한다.
- 동시발생 행렬을 PPMI 행렬로 변환하고 다시 차원을 감소 시킴으로써 거대한 희소벡터를 작은 밀집벡터로 변환할 수 있다.
