해당 포스팅은 '밑바닥부터 시작하는 딥러닝1'을 공부하고 정리, 요약한 글입니다. 모든 내용은 해당 도서를 기준으로 합니다.

◼️ 6.1 매개변수 갱신
◾ 6.1.3 SGD 단점
SGD는 매개변수의 기울기를 구해 기울어진 방향으로 매개변수 값을 갱신하는 일을 몇 번이고 반복해서 최적의 값에 다가갔다.
SGD는 단순하고 구현도 쉽지만 비효율적일 때가 있다.
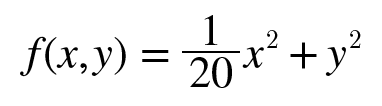

식 6.2는 그림 6-1의 왼쪽처럼 밥그릇을 x축 방향으로 늘인 모습이며 실제로 등고선은 오른쪽과 같이 x축 방향으로 늘인 타원으로 되어 있다. 식 6.2의 기울기를 그려보면 그림 6-2처럼 된다.

이 기울기는 y축 방향은 크고 x축 방향은 작다는 것이 특징이다.
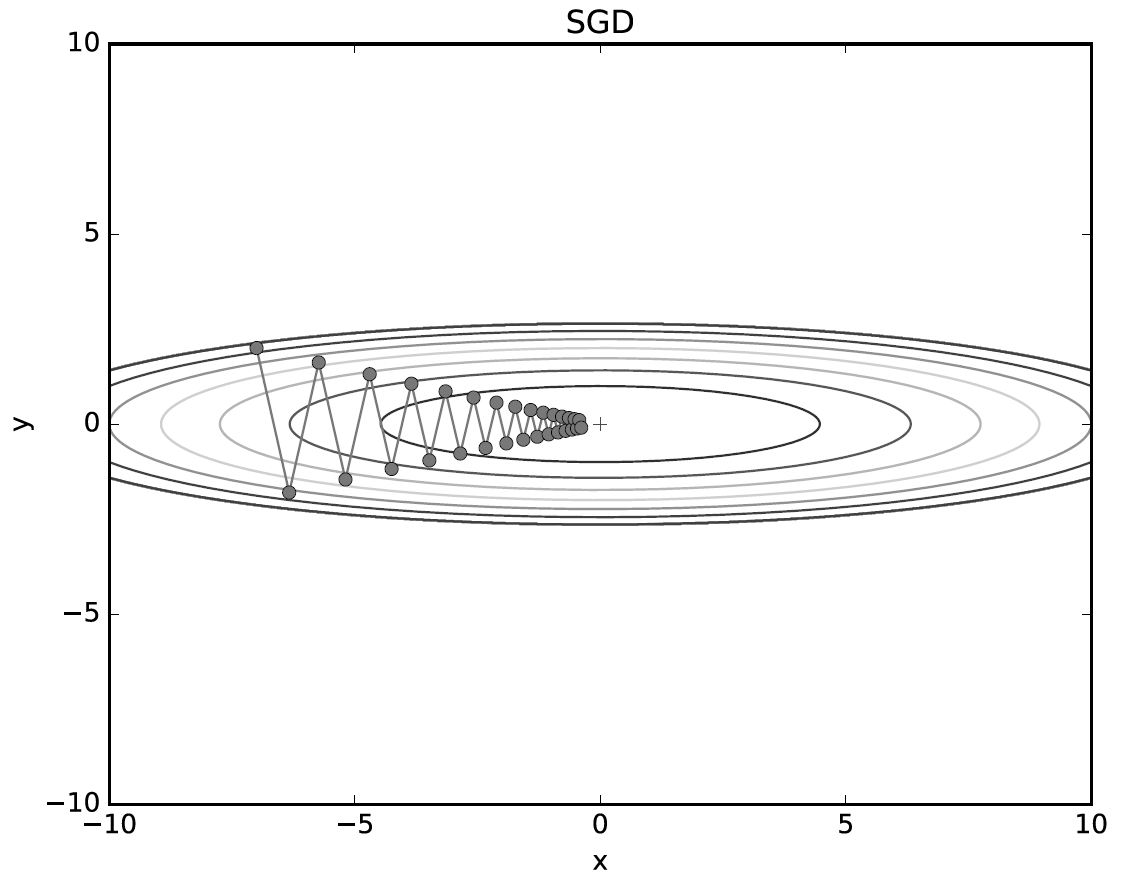
SGD는 그림 6-3과 같은 심하게 굽이진 움직임을 보여주는데 이는 비효율적인 움직임이다.
SGD의 단점은 비등방성 함수(방향에 따라 성질, 즉 기울기가 달라지는 함수)에서는 탐색 경로가 비효율적이라는 것이다.
SGD의 이런 단점을 개선 해 주는 방법으로는 모멘텀, AdaGrad, Adam이 있다.
◾ 6.1.4 모멘텀
모멘텀은 운동량을 뜻하는 단어로 다음과 같이 쓸 수 있다.
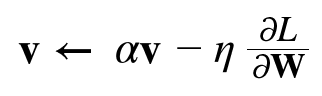

v라는 변수가 새로 나오는데 이는 물리에서 말하는 속도에 해당한다.
또 식 6.3의 αv항은 물체가 아무런 힘을 받지 않을 때 서서히 하강시키는 역할을 한다.
모멘텀의 구현은 다음과 같다.
# 모멘텀 클래스
class Momentum:
def __init__(self, lr=0.01, momentum=0.9):
self.lr = lr
self.momentum = momentum
self.v = None
def update(self, params, grads):
if self.v is None:
self.v = {}
for key, val in params.items():
self.v[key] = np.zeros_like(val)
for key in params.keys():
self.v[key] = self.momentum*self.v[key] - self.lr*grads[key]
params[key] += self.v[key]
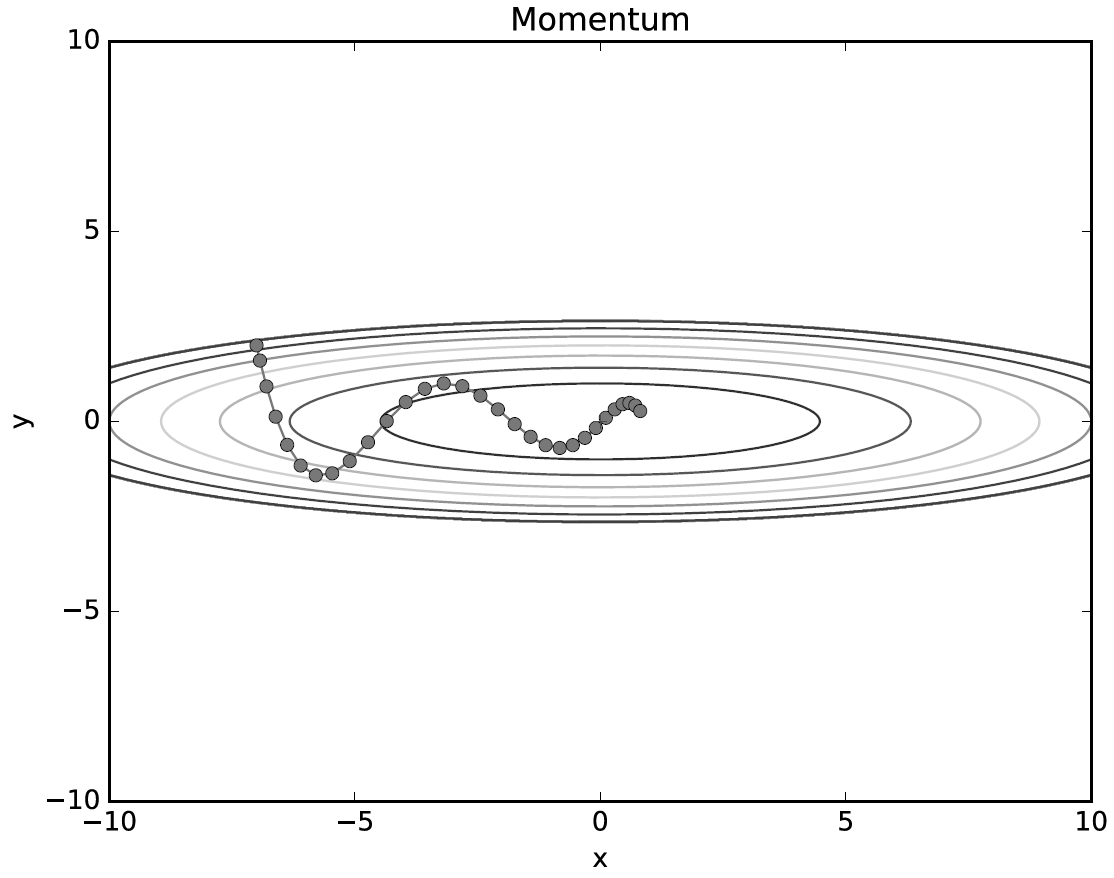
그림에서 보듯 모멘텀의 갱신 경로는 공의 그릇 바닥을 구르듯 움직인다. SGD와 비교하면 지그재그 정도가 덜한 것을 알 수 있다. 이는 x축의 힘은 아주 작지만 방향은 변하지 않아서 한 방향으로 일정하게 가속하기 때문이다. 거꾸로 y축의 힘은 크지만 위아래로 번갈아 받아서 상충하여 y축 방향의 속도는 안정적이지 않다.
◾ 6.1.5 AdaGrad
신경망 학습에서는 학습률 값이 중요하다. 이 값이 너무 작으면 학습 시간이 너무 길어지고 반대로 너무 크면 발산하여 학습이 제대로 이뤄지지 않는다.
이 학습률을 정하는 효과적 기술로 학습을 진행하면서 학습률을 점차 줄여가는 방법인, 학습률 감소가 있다.
학습률을 서서히 낮추는 가장 간단한 방법은 매개변수 전체의 학습률 값을 일괄적으로 낮추는 것이다. 이를 발전 시킨것이 AdaGrad이다. AdaGrad는 각각의 매개변수에 맞춤형 값을 만들어 준다.
AdaGrad는 개별 매개변수에 적응적으로 학습률을 조정하면서 학습을 진행한다. AdaGrad의 갱신 방법은 수식으로는 다음과 같다.
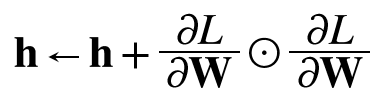

매개변수의 원소 중에서 많이 움직인(크게 갱신된) 원소는 학습률이 낮아진다는 뜻인데 다시 말해 학습률 감소가 매개변수의 원소마다 다르게 적용됨을 뜻한다.
class AdaGrad:
"""AdaGrad"""
def __init__(self, lr=0.01):
self.lr = lr
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] += grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)마지막 줄에서 1e-7이라는 작은 값은 self.h[key]에 0이 담겨 있어도 0으로 나누는 사태를 막아준다.
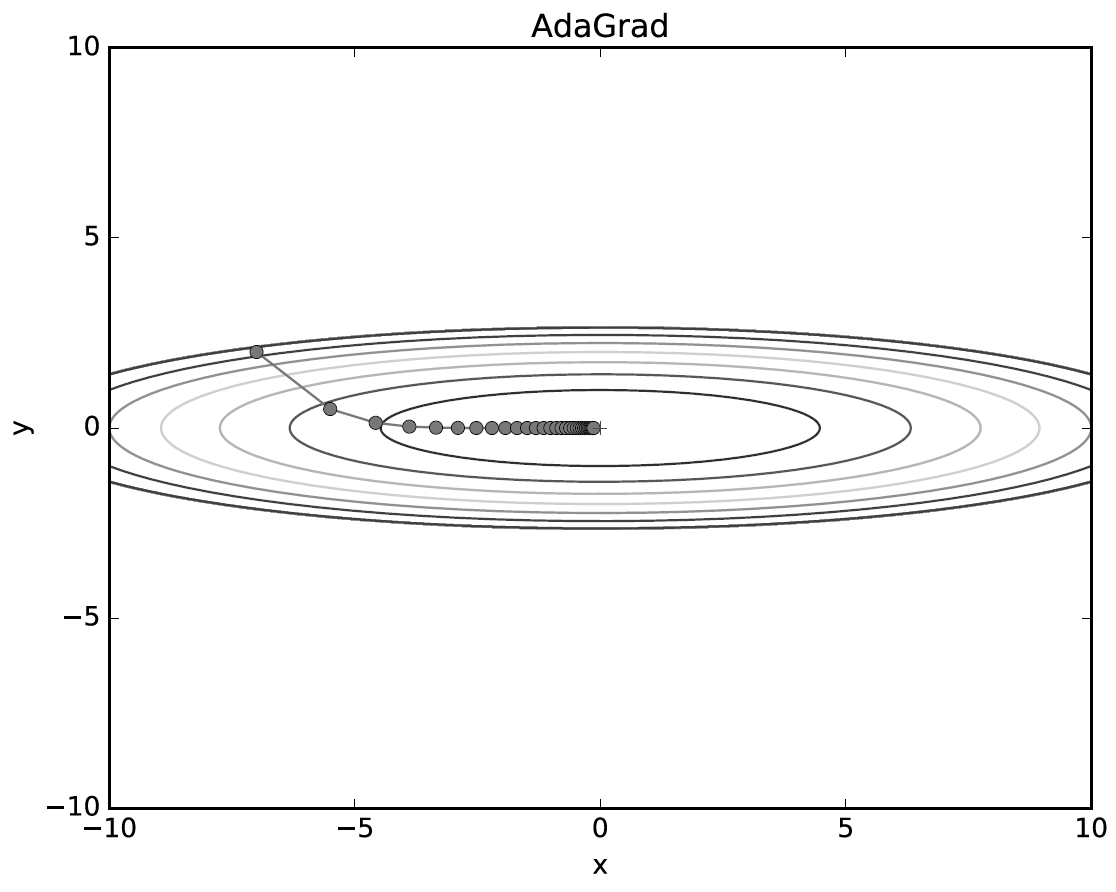
그림 6-6을 보면 최곳값을 향해 효율적으로 움직이는 것을 알 수 있다. y축 방향은 기울기가 커서 처음에는 크게 움직이지만 그 큰 움직임에 비례해 갱신 정도도 큰 폭으로 작아지도록 조정된다. 그래서 y축 방향으로 갱신 강도가 빠르게 약해지고 지그재그 움직임이 줄어든다.
◾ 6.1.6 Adam
모멘텀과 AdaGrad를 융합한 방법인 Adam이라는 기법도 있다.
Adam은 하이퍼파라미터의 편향 보정이 진행된다.
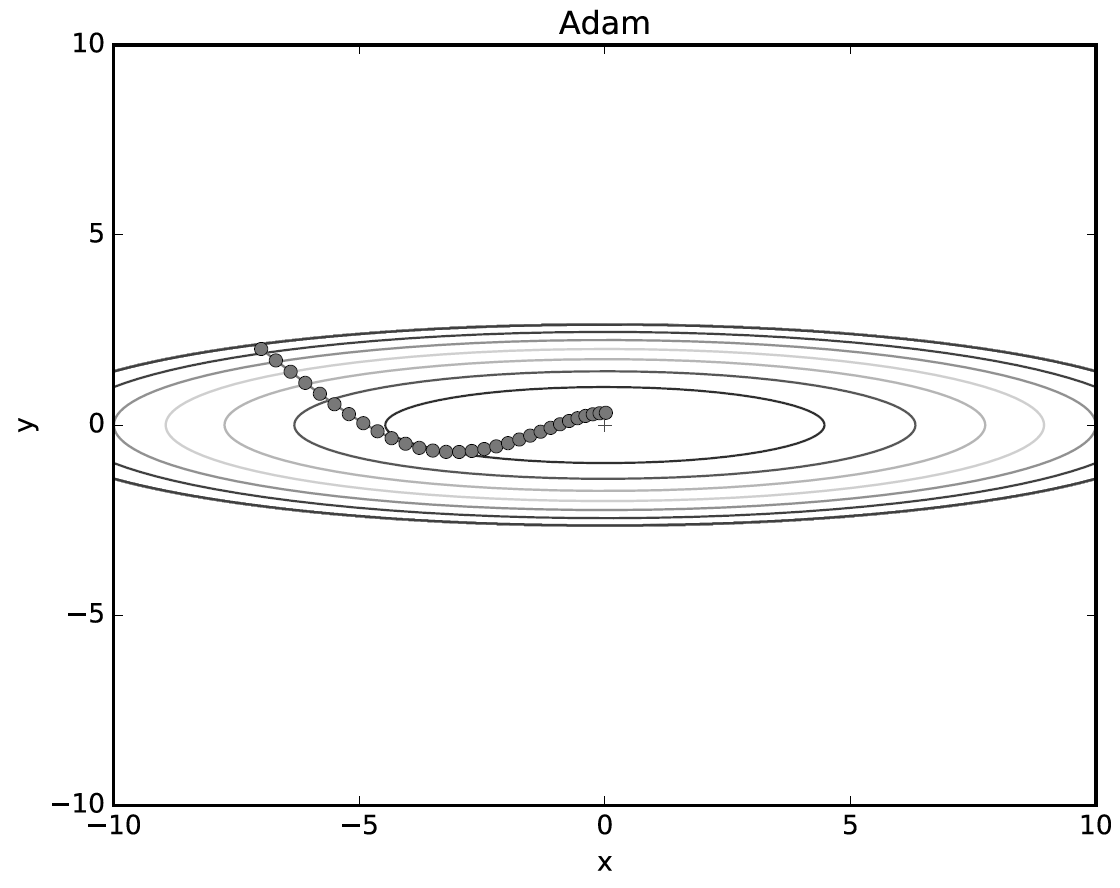
그림 6-7과 같이 Adam 갱신 과정도 그릇 바닥을 구르듯 움직인다. 모멘텀과 비슷한 패턴인데 모멘텀 때보다 공의 좌우 흔들림이 적다. 이는 학습의 갱신 강도를 적응적으로 조정해서 얻는 혜택이다.
◾ 6.1.7 어느 갱신 방법을 이용할 것인지

그림 6-8과 같이 사용한 기법에 따라 갱신 경로가 다르다. 풀어야 할 문제가 무엇이냐에 따라 달라지므로 주의해야 하며 하이퍼파라미터를 어떻게 설정하느냐에 따라서도 결과가 바뀐다.
◼️ 6.2 가중치 초깃값
◾ 6.2.1 초깃값을 0으로 했을 때
가중치의 초깃값을 모두 0으로 설정하면 학습이 올바로 이뤄지지 않는다.
◾ 6.2.2 은닉층의 활성화값 분포
은닉층의 활성화값의 분포를 관찰하면 중요한 정보를 얻을 수 있다.
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def ReLU(x):
return np.maximum(0, x)
def tanh(x):
return np.tanh(x)
input_data = np.random.randn(1000, 100) # 1000개의 데이터
node_num = 100 # 각 은닉층의 노드(뉴런) 수
hidden_layer_size = 5 # 은닉층 5개
activations = {} # 활성화 결과를 저장
x = input_data
for i in range(hidden_layer_size):
if i != 0:
x = activations[i-1]
w = np.random.randn(node_num, node_num) * 1
# w = np.random.randn(node_num, node_num) * 0.01
# w = np.random.randn(node_num, node_num) * np.sqrt(1.0 / node_num)
# w = np.random.randn(node_num, node_num) * np.sqrt(2.0 / node_num)
a = np.dot(x, w)
z = sigmoid(a)
# z = ReLU(a)
# z = tanh(a)
activations[i] = z활성화 함수로는 시그모이드 함수를 이용했으며 이 코드에서는 가중치의 분포에 주의해야 한다. 이 분포된 정도를 바꿔가며 활성화값들의 분포가 어떻게 변화하는지 관찰하는 것이 이 실험의 목적이다.

시그모이드 함수는 그 출력이 0에 가까워지자 그 미분은 0에 다가간다. 따라서 역전파의 기울기 값이 점점 작아지다가 사라진다. 이를 기울기 소실이라고 하며 층을 깊게 하는 딥러닝에서는 기울기 소실은 더 심각한 문제가 될 수 있다.
가중치의 표준편차를 0.01로 바꿔서 같은 실험을 반복하면 결과는 다음과 같다.

0.5 부근에 집중되어 있기 때문에 기울기 소실 문제는 일어나지 않지만 활성화값들이 치우쳤다는 것은 표현력 관점에서는 큰 문제가 있는 것이다.
다수의 뉴런이 거의 같은 값을 출력하고 있으니 뉴런을 여러 개 둔 의미가 없어진다는 뜻이다.
그래서 활성화값들이 치우치면 표현력을 제한한다는 관점에서 문제가 된다.

Xavier 초기값을 사용한 결과는 그림 6-13과 같다. 층이 깊어지면서 형태가 다소 일그러지지만 앞에서 본 방식보다는 확실히 넓게 분포됨을 알 수 있다.
◾ 6.2.3 ReLU를 사용할 때의 가중치 초깃값
Xavier 초깃값은 활성화 함수가 선형인 것을 전제로 이끈 결과이다. sigmoid 함수와 tanh 함수는 좌우 대칭이라 중앙 부근이 선형인 함수로 볼 수 있다. 반면 ReLU를 이용할 때는 ReLU에 특화된 초깃값을 이용해야 한다.

Xavier 초기값 결과는 층이 깊어지면서 치우침이 조금씩 커지기 때문에 기울기 소실 문제를 일으킨다. ReLU에 적합한 초기값인 He 초기값은 모든 층에서 균일하게 분포되었다.
층이 깊어져도 분포가 균일하게 유지되기에 역전파 때도 적절한 값이 나올 것으로 기대할 수 있다.
◼️ 6.3 배치 정규화
◾ 6.3.1 배치 정규화 알고리즘
배치 정규화는 각 층이 활성화를 적당히 퍼뜨리도록 강제해 보자는 아이디어에서 출발한 방법이다.
배치 정규화가 주목받는 이유는 다음과 같다.
- 학습을 빨리 진행할 수 있다.
- 초기값에 크게 의존하지 않는다
- 오버피팅을 억제한다.
배치 정규화의 기본 아이디어는 각 층에서의 활성화값이 적당히 분포 되도록 조정하는 것이다.

그림 6-16과 같이 데이터 분포를 정규화하는 배치 정규화(batch norm) 계층을 신경망에 삽입한다.
배치 정규화는 그 이름과 같이 학습 시 미니배치를 단위로 정규화 한다.

이 처리를 활성화 함수의 앞에 삽입함으로써 데이터 분포가 덜 치우치게 할 수 있다.
배치 정규화 계층마다 이 정규화된 데이터에 고유한 확대(scale)와 이동(shift)변환을 수행한다.

식에서 γ가 확대를 β가 이동을 담당하며 두 값은 각각 처음에 1, 0으로 시작하고 학습하면서 적합한 값으로 조정 해 간다.

◾ 6.3.2 배치 정규화의 효과
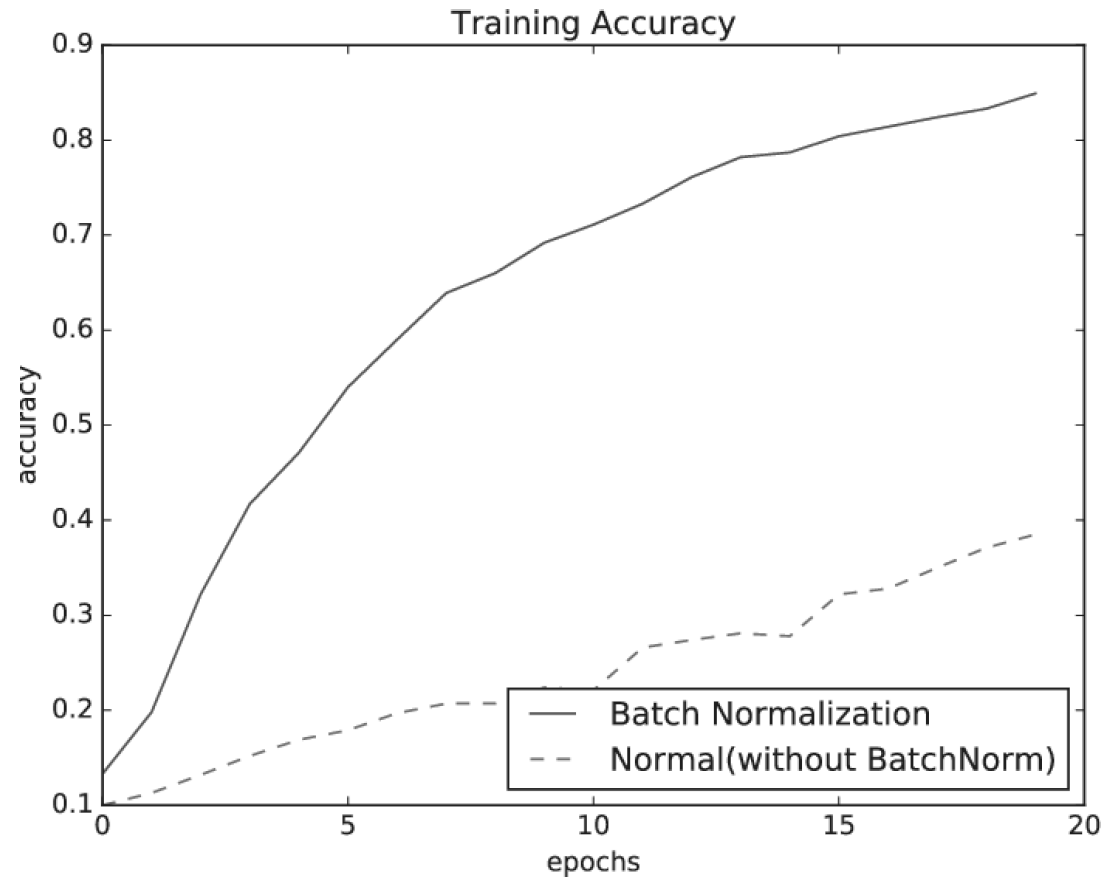
배치 정규화가 학습을 빨리 진전 시키고 있음을 그림 6-18을 통해 알 수 있다.

거의 모든 경우에서 배치 정규화를 사용할 때의 학습 진도가 빠른 것으로 나타난다.
◼️ 6.4 바른 학습을 위해
◾ 6.4.1 오버피팅
오버피팅은 매개변수가 많고 표현력이 높은 모델일 경우와 훈련 데이터가 적을 때 일어난다.
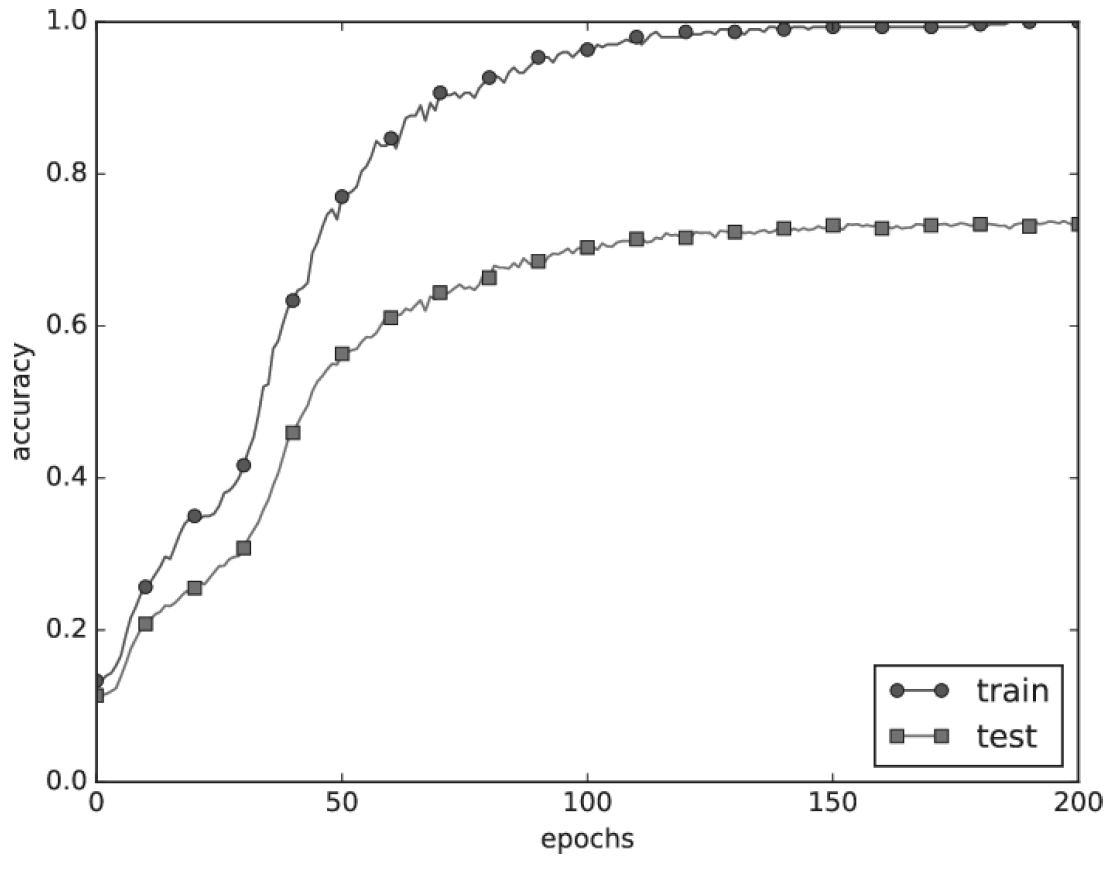
훈련 데이터를 사용하여 측정한 정확도는 100 에폭을 지나는 무렵부터 거의 100%임을 그림 6-20을 통해 알 수 있다. 하지만 시험 데이터에 대해서는 큰 차이를 보인다. 이처럼 정확도가 크게 벌어지는 것은 훈련 데이터에만 적응(fitting) 해 버린 결과이다.
◾ 6.4.2 가중치 감소
오버피팅 억제용으로 가중치 감소라는 방법이 있다.
학습 과정에서 큰 가중치에 대해서는 그에 상응하는 큰 페널티를 부과하여 오버피팅을 억제하는 방법이다. 원래 오버피팅은 가중치 매개변수의 값이 커서 발생하는 경우가 많기 때문이다.

가중치 감소를 이용하지 않은 그림 6-20과 비교하면 그 차이가 줄었음을 그림 6-21을 통해 알 수 있다.
◾ 6.4.3 드롭아웃
신경망 모델이 복잡해지면 가중치 감소만으로는 대응하기 어려워지는데 이때는 드롭아웃이라는 기법을 이용한다.
드롭아웃은 뉴런을 임의로 삭제하면서 학습하는 방법이다.
훈련 때 은닉층의 뉴런을 무작위로 골라 삭제한다.
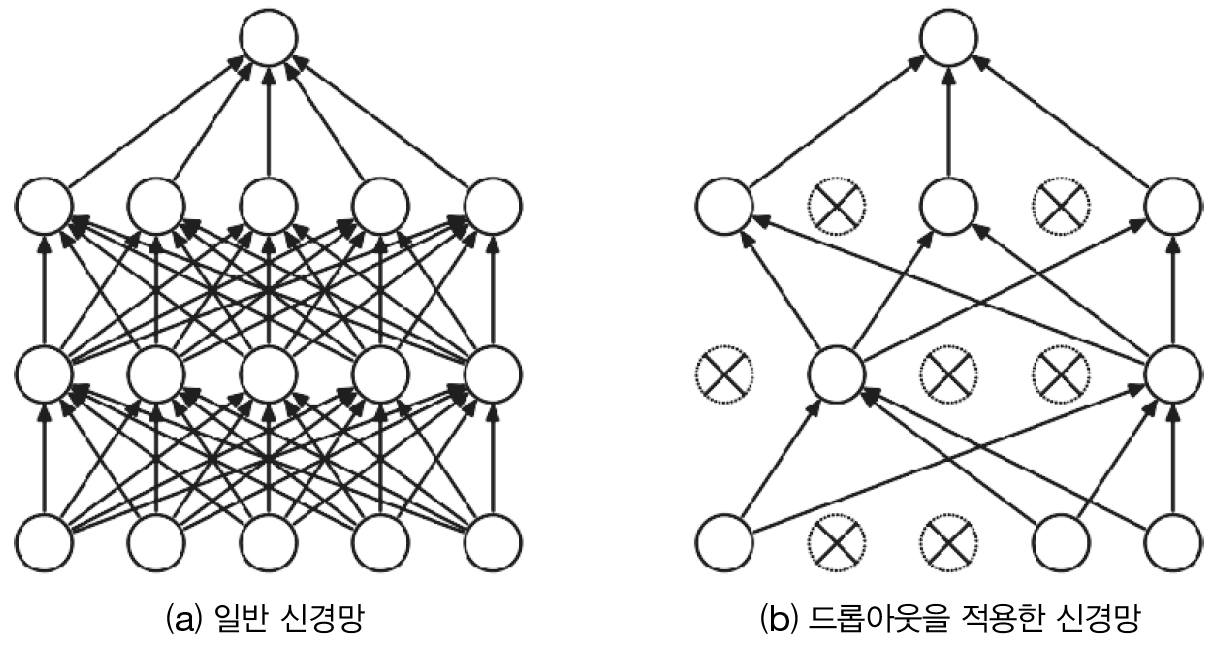
훈련 때는 데이터를 흘릴 때마다 삭제할 뉴런을 무작위로 선택하고 시험 때는 모든 뉴런에 신호를 전달한다. 단, 시험 때는 각 뉴런의 출력에 훈련 때 삭제한 비율을 곱해 출력한다.
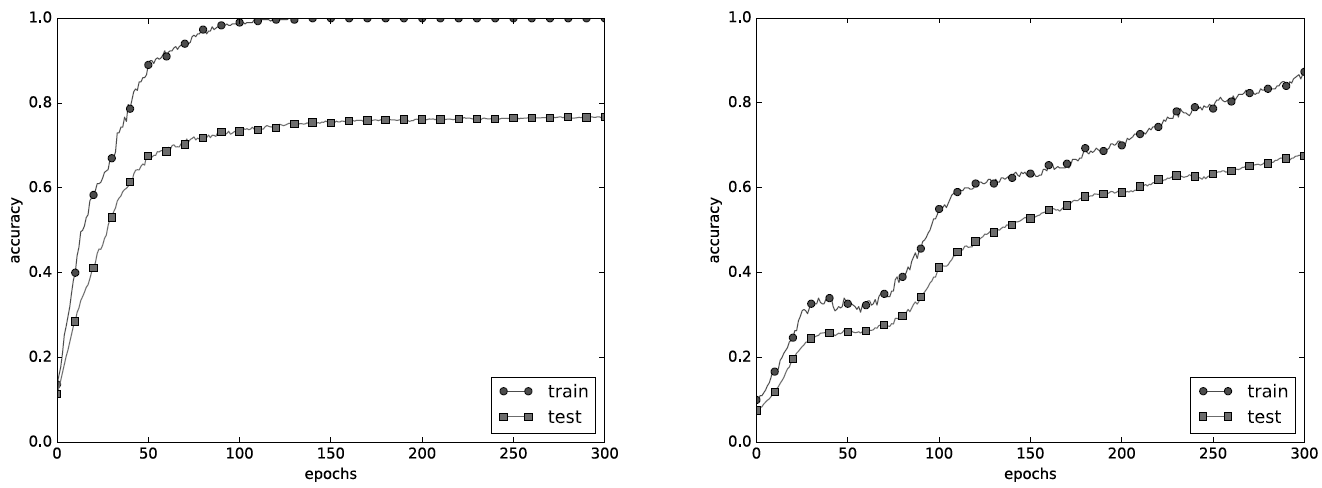
그림 6-23은 왼쪽은 드롭아웃 없이, 오른쪽은 드롭아웃을 적용한 결과이다.
드롭아웃을 적용하니 훈련 데이터와 시험 데이터에 대한 정확도 차이가 줄었다. 또, 훈련 데이터에 대한 정확도가 100%에 도달하지도 않게 되었다.
이처럼 드롭아웃을 이용하면 표현력을 높이면서도 오버피팅을 억제할 수 있다.
◼️ 6.5 적절한 하이퍼파라미터 값 찾기
◾ 6.5.1 검증 데이터
하이퍼파라미터의 성능을 평가할 때는 시험 데이터를 사용해서는 안된다. 시험 데이터를 사용하여 하이퍼파라미터를 조정하게 되면 하이퍼파라미터 값이 시험 데이터에 오버피팅되기 때문이다.
그래서 하이퍼파라미터를 조정할 때는 하이퍼파라미터 전용 확인 데이터가 필요하다. 하이퍼파라미터 조정용 데이터를 일반적으로 검증 데이터라고 부른다.
◾ 6.5.2 하이퍼파라미터 최적화
하이퍼파라미터를 최적화 할 때의 핵심은 하이퍼파라미터의 최적 값이 존재하는 범위를 조금씩 줄여간다는 것이다.
대략적인 범위를 설정하고 그 범위에서 무작위로 하이퍼파라미터 값을 골라(샘플링)낸 후 그 값으로 정확도를 평가한다.
하이퍼파라미터의 범위는 대략적으로 지정하는 것이 효과적이다. 보통은 10의 거듭제곱 단위로 범위를 지정한다.
하이퍼파라미터를 최적화 할 때는 딥러닝 학습에는 오랜시간이 걸린다는 점에 주의해야 한다.
- 0단계
: 하이퍼파라미터 값의 범위를 설정한다.
- 1단계
: 설정된 범위에서 하이퍼파라미터의 값을 무작위로 추출한다.
- 2단계
: 1단계에서 샘플링한 하이퍼파라미터 값을 사용하여 학습하고 검증 데이터로 정확도를 평가한다.
- 3단계
: 1단계와 2단계를 특정 횟수를 반복하며 그 정확도의 결과를 보고 하이퍼파라미터의 범위를 좁힌다.
위 단계들을 반복하여 하이퍼파라미터의 범위를 좁히고 어느 정도 좁아지면 그 압축한 범위에서 값을 하나 골라낸다.
◾ 6.5.3 하이퍼파라미터 최적화 구현하기
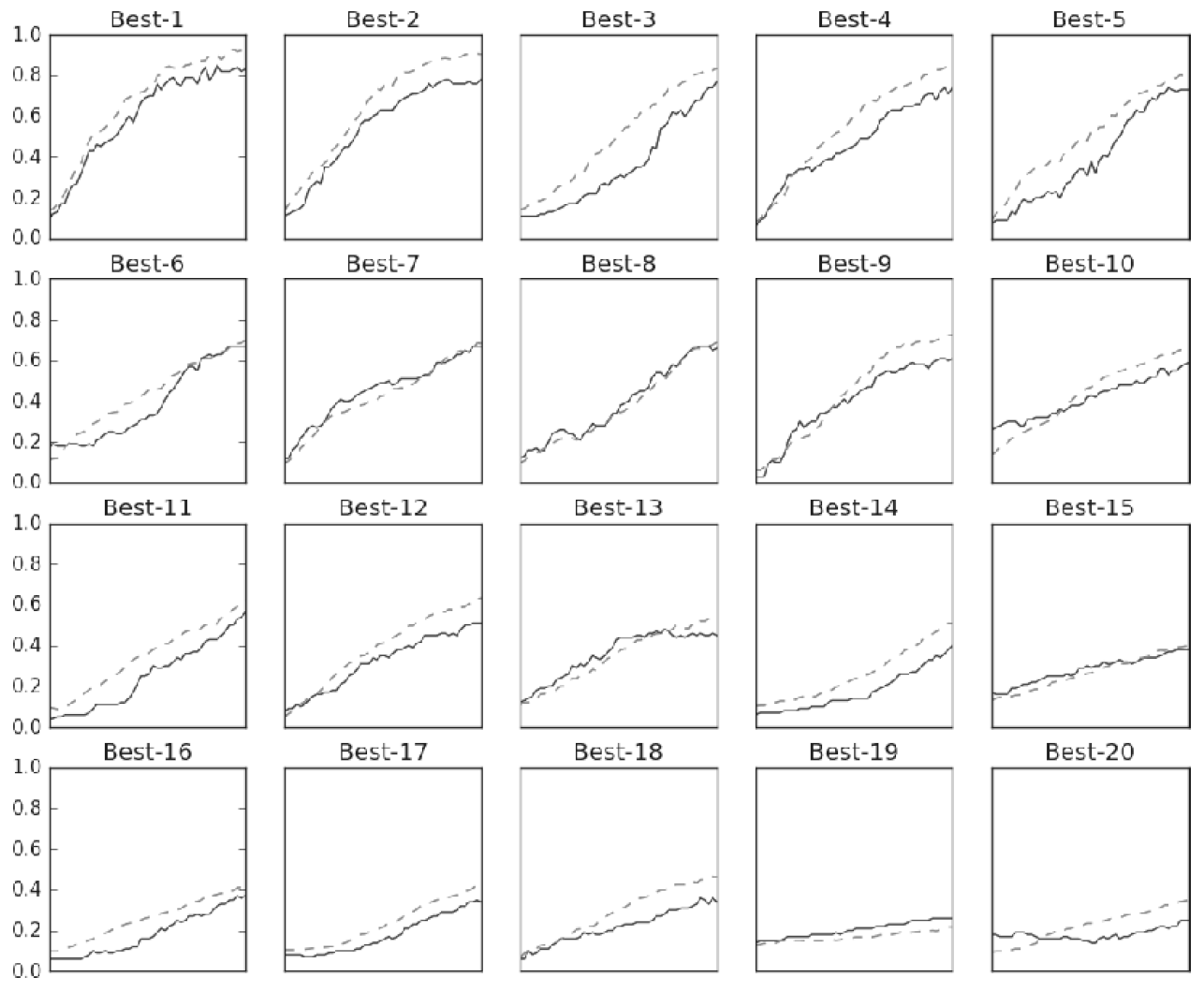
가중치 감소 계수의 범위를 10^-8~10^-4, 학습률의 범위를 10^-6~10^-2로 하여 실험하면 결과는 그림 6-24처럼 된다.
이 결과를 보면 학습이 잘 진행될 때의 학습률은 0.001~0.01, 가중치 감소 계수는 10^-8~10^-6 정도라는 것을 알 수 있다.
이처럼 잘될 것 같은 값의 범위를 관찰하고 범위를 좁혀간다. 그런 다음 그 축소된 범위로 똑같은 작업을 반복하는 것이다. 이렇게 적절한 값이 위치한 범위를 좁혀가다가 특정 단계에서 최종 하이퍼파라미터 값을 하나 선택한다.
◼️ 정리
- 매개변수 갱신 방법에는 확률적 경사 하강법 (SGD) 외에도 모멘텀, AdaGrad, Adam 등이 있다.
- 가중치 초깃값을 정하는 방법은 올바른 학습을 하는 데 매우 중요하다
- 배치 정규화를 이용하면 학습을 빠르게 진행할 수 있으며 초깃값에 영향을 덜 받게 된다.
- 오버피팅을 억제하는 정규화 기술로는 가중치 감소와 드롭아웃이 있다.
- 하이퍼파라미터 값 탐색은 최적 값이 존재할 법한 범위를 점차 좁히면서 하는 것이 효과적이다.
