해당 포스팅은 '밑바닥부터 시작하는 딥러닝1'을 공부하고 정리, 요약한 글입니다. 모든 내용은 해당 도서 기준입니다.

◼️ 3.1 퍼셉트론에서 신경망으로
◾ 3.1.1 신경망의 예

신경망을 그림으로 나타내면 그림3-1처럼 된다. 가장 왼쪽 줄을 입력층, 맨 오른쪽 줄을 출력층, 중간 줄을 은닉층이라고 한다. 은닉층의 뉴런은 사람 눈에는 보이지 않는다.
◾ 3.1.2 퍼셉트론 복습
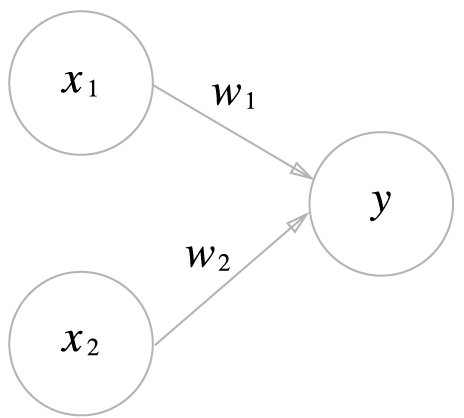
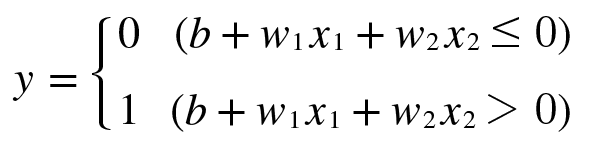
위는 x1와 x2라는 두 신호를 입력 받아 y를 출력하는 퍼셉트론이다. 이를 간결한 형태로 다시 작성하기 위해 조건 분기 동작(0을 넘으면 1을 출력하고 그렇지 않으면 0을 출력)을 하나의 함수 h(x)로 나타내면 다음과 같다.


식 3.2는 입력 신호의 총 합이 h(x)라는 함수를 거쳐 변환되어 그 변환된 값이 y의 출력이 됨을 보여준다. 식 3.3의 h(x) 함수는 입력이 0을 넘으면 1을 돌려주고 그렇지 않으면 0을 돌려 준다.
◾ 3.1.3 활성화 함수의 등장
입력 신호의 총 합을 출력 신호로 변환하는 함수를 활성화 함수라고 한다. 입력 신호의 총 합이 활성화를 일으키는지를 정하는 역할을 한다.
식 3.2는 가중치가 곱해진 입력 신호의 총 합을 계산하고 그 합을 활성화 함수에 입력해 결과를 내는 2단계로 처리된다.


식 3.4는 가중치가 달린 입력 신호와 편향의 총 합을 계산하고 이를 α라고 한다. 식 3.5는 α를 함수 h()에 넣어 y를 출력하는 흐름이다.
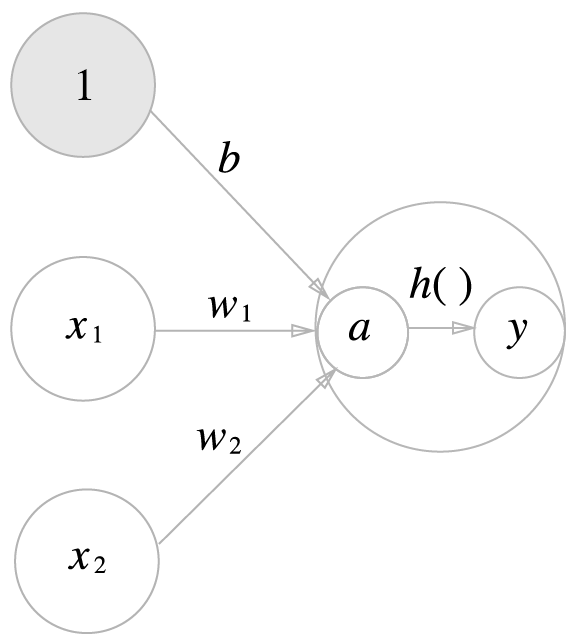
위 그림에서 기존 뉴런의 원을 키우고 그 안에 활성화 함수의 처리 과정을 명시적으로 그려 넣었으며, 가중치 신호를 조합한 결과가 α라는 노드가 되고 활성화 함수 h()를 통과하여 y라는 노드로 변환되는 과정이 나타나있다.

그림 3-5의 왼쪽처럼 뉴런을 하나의 원으로 그리지만, 신경망의 동작을 더 명확히 드러내고자 할 때 오른쪽 그림처럼 활성화 처리 과정을 명시하기도 한다.
◼️ 3.2 활성화 함수
활성화 함수는 임계값을 경계로 출력이 바뀌는데 이런 함수를 계단 함수라고 한다.
따라서 퍼셉트론에서는 활성화 함수로 계단 함수를 이용한다고 할 수 있다.
◾ 3.2.1 시그모이드 함수
신경망에서 자주 이용하는 활성화 함수인 시그모이드 함수는 식 3.6으로 나타낸다.

◾ 3.2.2 계단 함수 구현하기
계단 함수는 입력이 0을 넘으면 1을 출력하고 그 외에는 0을 출력하는 함수이다.
이를 파이썬으로 구현하면 다음과 같다.

이는 x가 실수만 받아들이지만 넘파이 배열도 지원하도록 수정하면 아래와 같다.

파이 배열에 부등호 연산을 수행하면 배열의 원소 각각에 부등호 연산을 수행한 bool 배열이 생성된다. y를 int형으로 바꿔주기 위해서는 astype() 메서드를 이용하면 된다. bool을 int로 변환하면 True는 1로, False는 0으로 변환된다.
◾ 3.2.3 계단 함수의 그래프
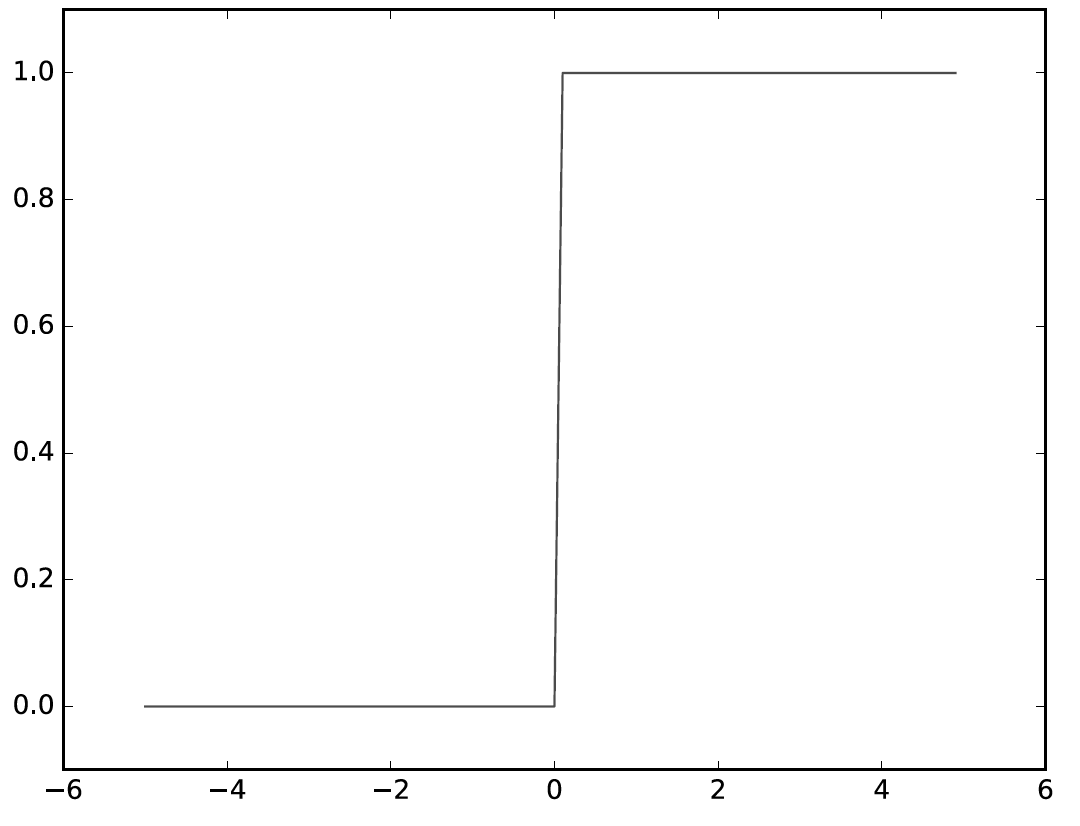
위 그림처럼 값이 바뀌는 형태가 계단처럼 생겼기 때문에 계단 함수로 불린다.
◾ 3.2.4 시그모이드 함수 구현하기
시그모이드 함수는 파이썬으로 다음과 같이 작성할 수 있다.
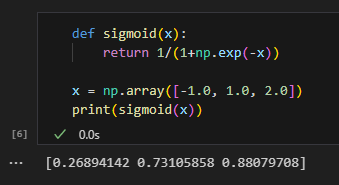
이 코드는 x가 넘파이 배열이어도 올바른 결과가 나오는데 이는 브로드캐스트 덕분이다. 브로드캐스트 기능이란 넘파이 배열과 스칼라 값의 연산을 넘파이 배열의 원소 각각과 스칼라 값의 연산으로 바꿔 수행하는 것이다. 스칼라 값과 넘파이 배열의 각 원소 사이에서 연산이 이뤄지고, 연산 결과가 넘파이 배열로 출력 된다.
◾ 3.2.5 시그모이드 함수와 계단 함수 비교

시그모이드 함수와 계단 함수를 비교했을 때 가장 큰 차이점은 매끄러움이다. 시그모이드 함수의 이 매끈함이 신경망 학습에서 아주 중요한 역할을 하게 된다.
또, 계단함수가 0과 1 중 하나의 값만 돌려주는 반면 시그모이드 함수는 실수를 돌려준다는 점도 다르다.
다시 말해, 퍼셉트론에서는 뉴런 사이에 0 또는 1이 흘렀다면 신경망에서는 연속적인 실수가 흐른다.
그림 3-8을 큰 관점에서 보면 둘은 같은 모양이라고 할 수 있다. 둘 다 입력이 작을 때의 출력은 0에 가깝고, 입력이 커지면 출력이 1에 가까워 지는 구조이기 때문이다.
즉, 계단 함수와 시그모이드 함수는 입력이 중요하면 큰 값을 출력하고 입력이 중요하지 않으면 작은 값을 출력한다. 또, 입력이 아무리 작거나 커도 출력은 0에서 1 사이라는 것도 둘의 공통점이다.
◾ 3.2.6 비선형 함수
계단 함수와 시그모이드 함수는 비선형 함수이다.
출력이 입력의 상수 배만큼 변하는 함수를 선형 함수라고 하며 곧은 1개의 직선이 된다.
하지만 비선형 함수는 문자 그대로 선형이 아닌 함수로, 직선 1개로는 그릴 수 없는 함수를 말한다.
선형 함수의 문제는 층을 아무리 깊게 해도 은닉층이 없는 네트워크로도 똑같은 기능을 할 수 있다는 데에 있다. 따라서 선형 함수를 이용하면 신경망의 층을 깊게 하는 의미가 없기 때문에, 신경망에서는 활성화 함수로 비선형 함수를 사용해야 한다.
◾ 3.2.7 ReLU 함수
신경망 분야에서 최근에는 ReLU 함수를 활성화 함수로서 주로 이용한다.



위처럼 파이썬에서는 넘파이의 maximun 함수를 사용해 ReLU 함수를 구현할 수 있다.
◼️ 3.3 다차원 배열의 계산
◾ 3.3.1 다차원 배열
숫자가 한 줄로 늘어선 것이나 직사각형으로 늘어놓은 것, 3차원으로 늘어놓은 것이나 N차원으로 나열하는 것을 통틀어 다차원 배열이라고 한다.
배열의 차원 수는 np.dim() 함수로 확인할 수 있다. 또, 배열의 형상은 인스턴스 변수인 shape으로 알 수 있다.
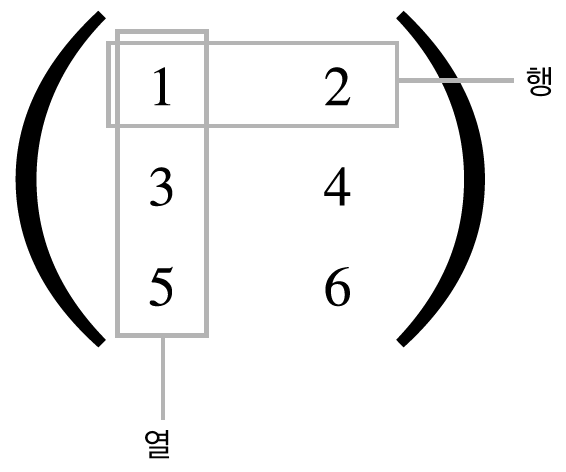
2차원 배열은 특히 행렬이라고 부르고 그림 3-10과 같이 배열의 가호 방향을 행(row), 세로 방향을 열(column)이라고 한다.
◾ 3.3.2 행렬의 곱
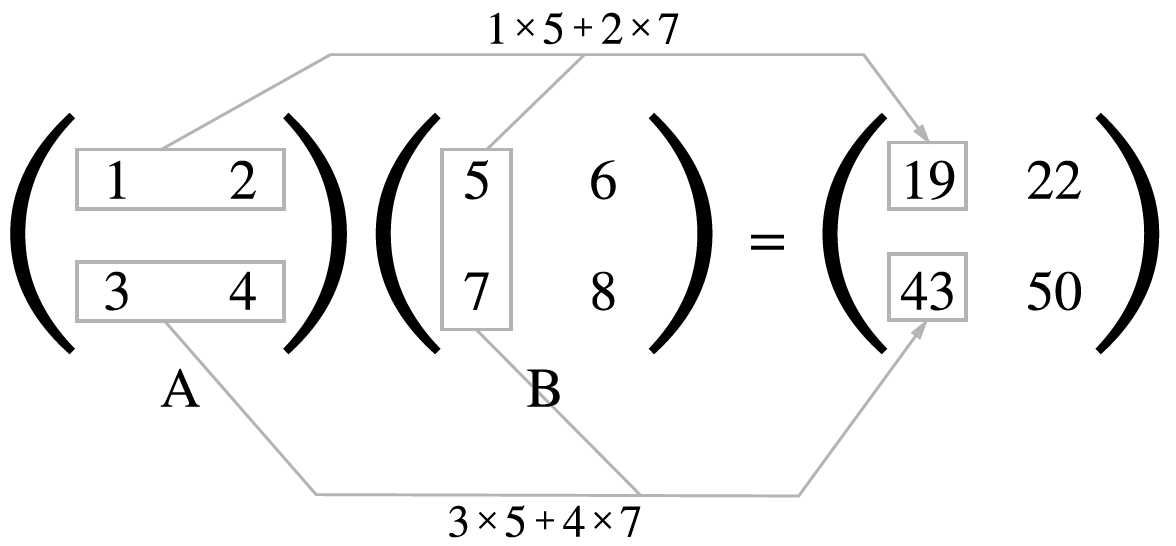
위 그림처럼 행렬 곱은 왼쪽 행렬의 행과 오른쪽 행렬의 열을 원소별로 곱하고 그 값들을 더해서 계산한다.

이 코드에서 A와 B는 2x2 행렬이며 이들 두 행렬의 곱은 넘파이 함수 np.dot()으로 계산한다.
행렬의 곱에서는 피연산자의 순서가 다르면 결과도 다르다. 행렬 A의 1번째 차원의 원소 수(열 수)와 행렬 B의 0번째 차원의 원소 수(행 수)가 같아야 하며 이 값이 다르면 행렬의 곱을 계산할 수 없다.
◾ 3.3.3 신경망에서의 행렬 곱
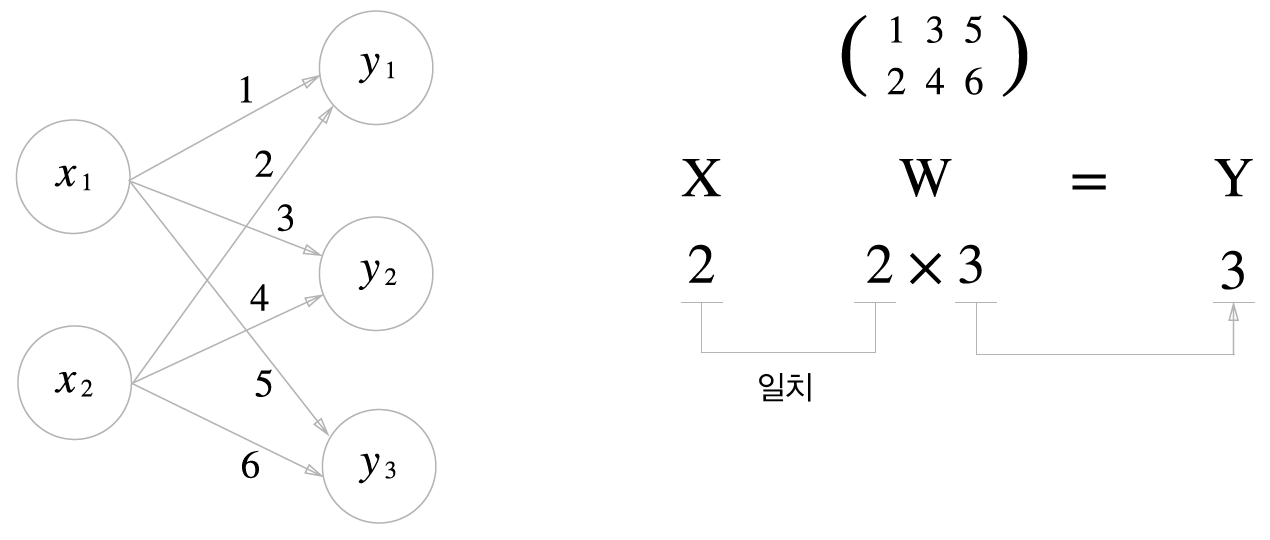

다차원 배열의 스칼라곱을 구해주는 np.dot 함수를 사용하면 이처럼 단번에 결과 Y를 계산할 수 있다.
행렬의 곱으로 한꺼번에 계산해주는 기능은 신경망을 구현할 때 매우 중요하다고 말할 수 있다.
◼️ 3.4 3층 신경망 구현하기
◾ 3.4.1 표기법 설명
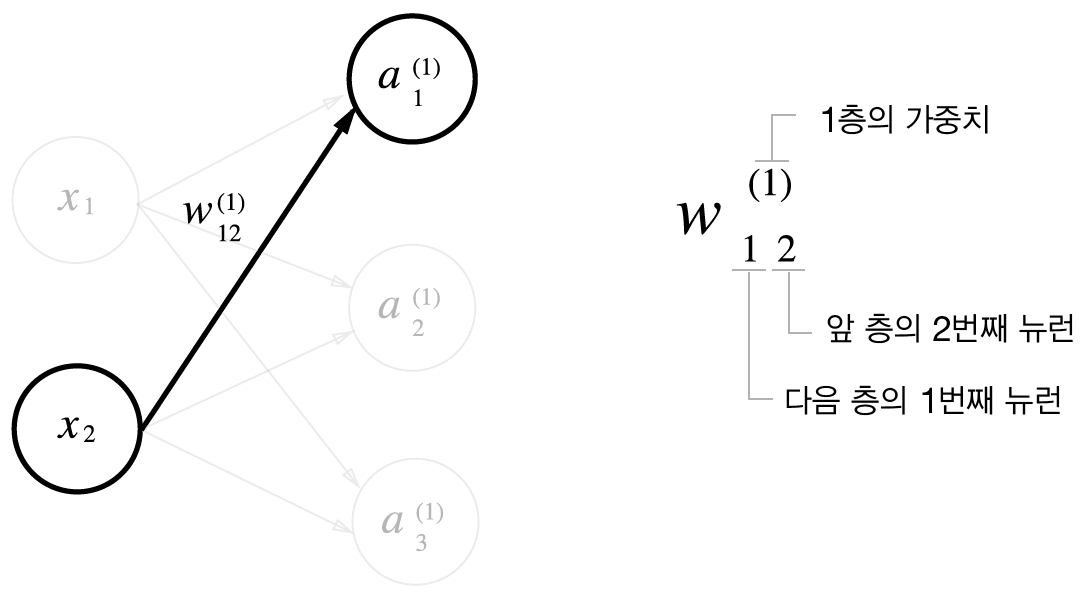
그림 3-16은 입력층의 뉴런 x2에서 다음 층 뉴런 a(1)1로 향하는 선 위에 가중치를 표시하고 있다.
가중치와 은닉층 뉴런의 오른쪽 위에는 (1)이 붙어 있으며 이는 1층 가중치, 1층 뉴런임을 의미한다.
가중치의 오른쪽 아래 두 숫자는 차례로 다음 층 뉴런과 앞 층 뉴런의 인덱스 번호이다.
◾ 3.4.2. 각 층의 신호 전달 구현하기
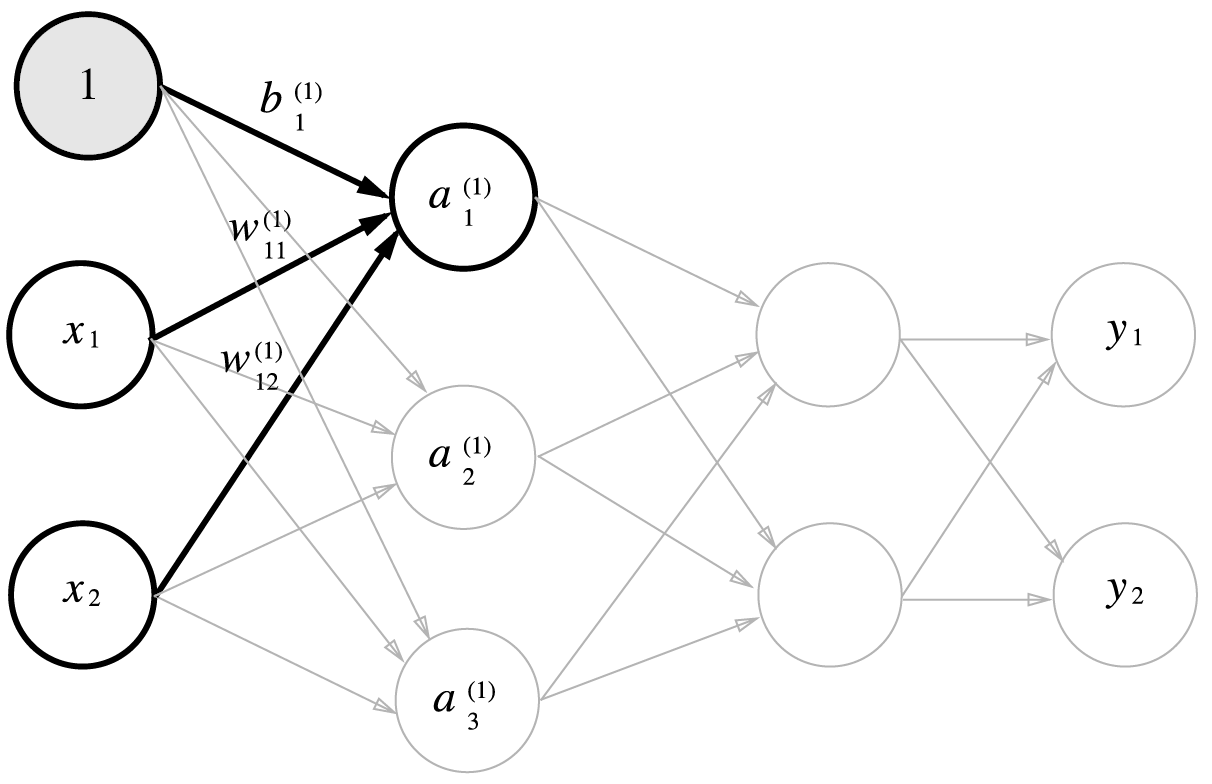
a(1)1을 수식으로 나타내면 다음과 같다.
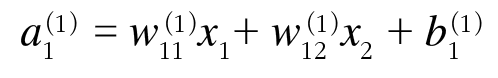
여기서 행렬의 곱을 이용하면 1층의 가중치 부분을 다음 식처럼 간소화 할 수 있다.

식 3.9를 파이썬으로 구현하면 아래와 같다.


그림 3-18과 같이 은닉층에서 가중치 합을 α로 표기하고 활성화 함수 h()로 변환된 신호를 z로 표기한다. 여기서 활성화 함수로 시그모이드 함수를 사용하기로 한다.
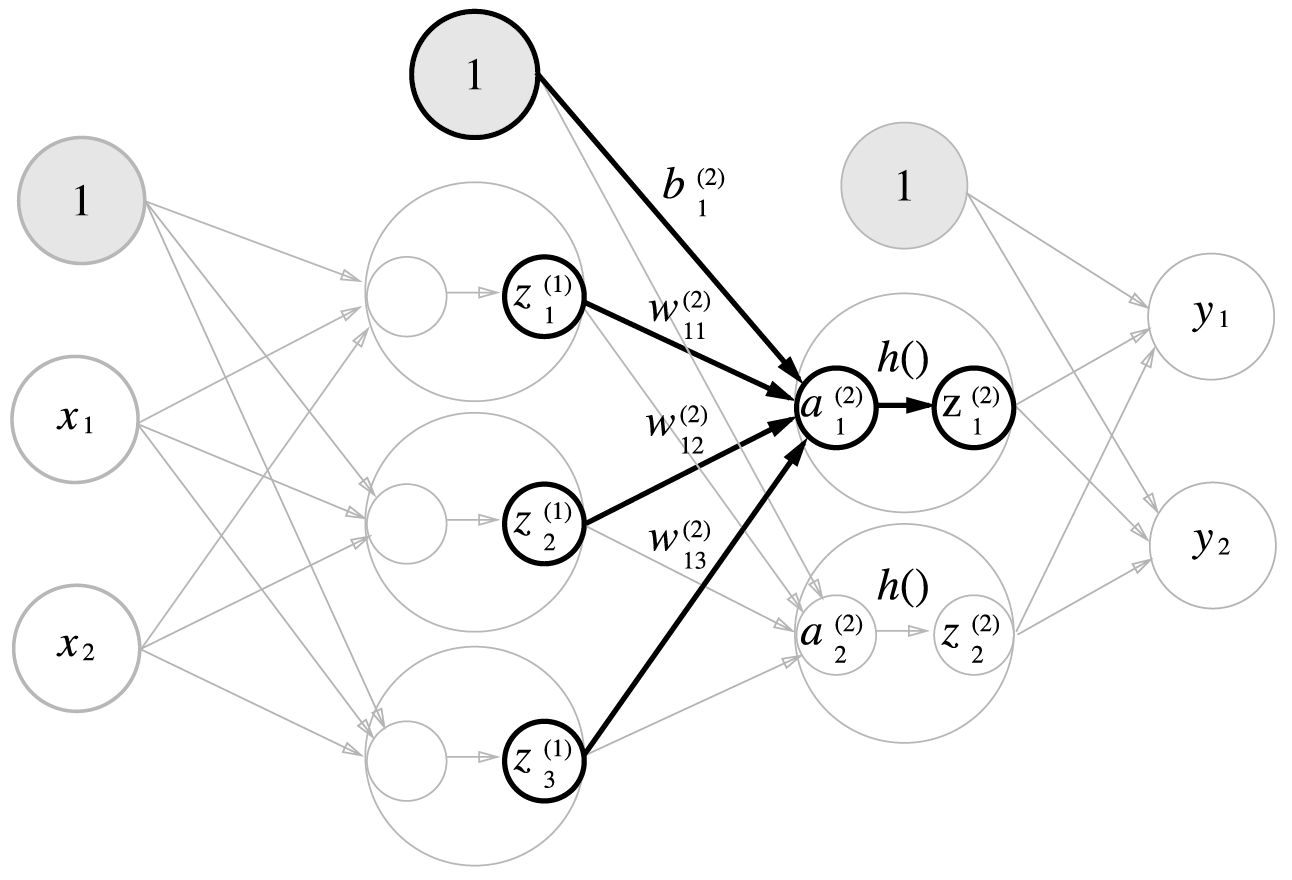

이는 1층의 출력 Z1이 2층의 입력이 된다는 점을 제외하면 이전 구현과 동일하지만 활성화 함수만 지금까지의 은닉층과 다르다.


여기선 항등 함수인 identity_function()을 정의하고 이를 출력층의 활성화 함수로 이용했다. 항등 함수는 입력을 그대로 출력함수이다.
그림 3-20에서는 출력층의 활성화 함수를 시그마로 표시하여 은닉층의 활성화 함수 h()와는 다름을 명시했다.
◾ 3.4.3 구현 정리
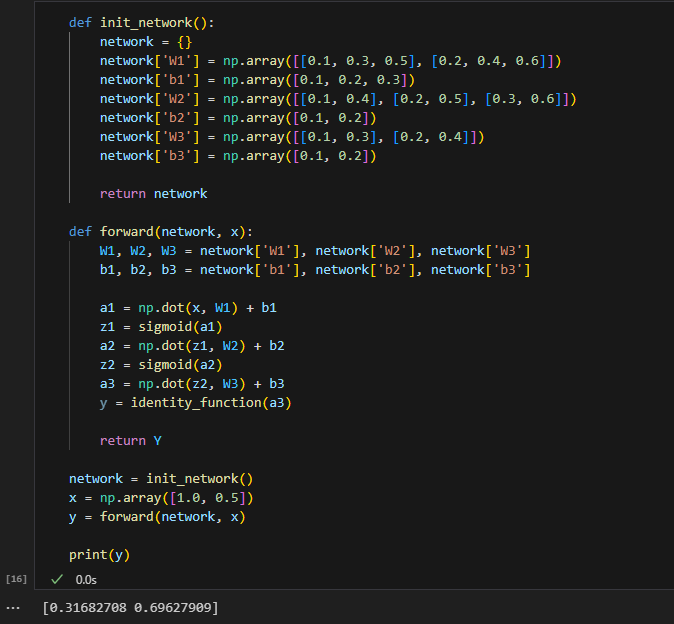
신호가 순방향으로 전달되기 때문에 순전파의 의미로 forward로 함수 이름을 정했다.
◼️ 3.5 출력층 설계하기
◾ 3.5.1 항등 함수와 소프트맥스 함수 구현하기
항등 함수는 입력을 그대로 출력하기 때문에 입력과 출력이 항상 같다.
항등 함수에 의한 변환은 은닉층에서의 활성화 함수와 마찬가지로 화살표로 그린다.
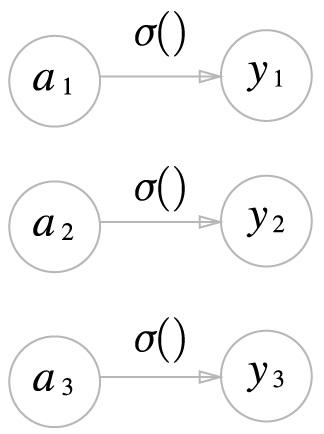
분류에서 소프트 맥스는 다음과 같다.
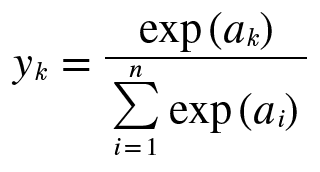
n은 출력층의 뉴런수, yk는 그 중 k번째 출력임을 의미한다.
◾ 3.5.2 소프트맥스 함수 구현 시 주의점
softmax() 함수의 코드는 컴퓨터로 계산할 때는 오버플로 문제가 있다. 지수 함수는 쉽게 아주 큰 값을 뱉는데 이런 큰 값 끼리 나눗셈을 하면 결과 수치가 불안정 해 진다.
다시 말해 표현할 수 있는 범위가 한정되어 너무 큰 값은 표현할 수 없다는 문제가 발생한다.
이것을 오버플로(overflow)라고 하며 컴퓨터로 수치를 계산할 때 주의해야 한다.
이 문제를 해결하도록 소프트맥스 함수를 개선하면 아래와 같다.

이는 소프트맥스의 지수 함수를 계산할 때 어떤 정수를 더해도 결과는 바뀌지 않는다는 것을 말하고 있다.
아무런 조치 없이 그냥 계산하면 nan이 출력되기 때문에 입력 신호 중 최대값을 빼주면 올바르게 계산할 수 있다.
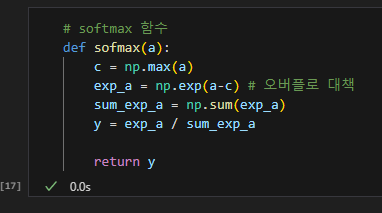
◾ 3.5.3 소프트맥스 함수의 특징
소프트맥스 함수의 출력은 0에서 1.0 사이의 실수이며 소프트맥스 함수 출력의 총합은 1이다. 출력 총합이 1이 된다는 건 소프트맥스 함수의 중요한 성질이다.
이 성질 덕분에 소프트맥스 함수의 출력을 확률로 해석할 수 있다. 소프트맥스 함수를 이용함으로써 문제를 확률적으로 대응할 수 있게 되는 것이다.
소프트맥스 함수를 적용해도 각 원소의 대소 관계는 변하지 않으며, 신경망을 이용한 분류에서는 일반적으로 가장 큰 출력을 내는 뉴런에 해당하는 클래스로만 인식한다. 그리고 소프트맥스 함수를 적용해도 출력이 가장 큰 뉴런의 위치는 달라지지 않는다.
결과적으로 신경망으로 분류할 때는 출력층의 소프트맥스 함수를 생략해도 된다. 실제로 현업에서도 자원 낭비를 줄이고자 출력층의 소프트맥스 함수는 생략하는 것이 일반적이다.
◾ 3.5.4 출력층의 뉴런 수 정하기
출력층의 뉴런 수는 풀고자 하는 문제에 맞게 적절히 정해야 한다.
◼️ 3.6 손글씨 숫자 인식
◾ 3.6.1 MNIST 데이터셋
28x28 사이즈의 1 채널 이미지로, 학습 데이터 6만장, 테스트 데이터 1만장으로 구성되어 있는 손글씨 분류 데이터셋이다.
◾ 3.6.2 신경망의 추론 처리
import sys, os
sys.path.append(os.pardir)
import numpy as np
import pickle
from dataset.mnist import load_mnist
from common.functions import sigmoid, softmax
def get_data():
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, flatten=True, one_hot_label=False)
return x_test, t_test
def init_network():
with open("sample_weight.pkl", 'rb') as f:
network = pickle.load(f)
return network
def predict(network, x):
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
z2 = sigmoid(a2)
a3 = np.dot(z2, W3) + b3
y = softmax(a3)
return y
x, t = get_data()
network = init_network()
accuracy_cnt = 0
for i in range(len(x)):
y = predict(network, x[i])
p= np.argmax(y) # 확률이 가장 높은 원소의 인덱스를 얻는다.
if p == t[i]:
accuracy_cnt += 1
print("Accuracy:" + str(float(accuracy_cnt) / len(x)))◾ 3.6.3 배치 처리
import sys, os
sys.path.append(os.pardir)
import numpy as np
import pickle
from dataset.mnist import load_mnist
from common.functions import sigmoid, softmax
def get_data():
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, flatten=True, one_hot_label=False)
return x_test, t_test
def init_network():
with open("sample_weight.pkl", 'rb') as f:
network = pickle.load(f)
return network
def predict(network, x):
w1, w2, w3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
a1 = np.dot(x, w1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, w2) + b2
z2 = sigmoid(a2)
a3 = np.dot(z2, w3) + b3
y = softmax(a3)
return y
x, t = get_data()
network = init_network()
batch_size = 100 # 배치 크기
accuracy_cnt = 0
for i in range(0, len(x), batch_size):
x_batch = x[i:i+batch_size]
y_batch = predict(network, x_batch)
p = np.argmax(y_batch, axis=1)
accuracy_cnt += np.sum(p == t[i:i+batch_size])
print("Accuracy:" + str(float(accuracy_cnt) / len(x)))
◼️ 정리
이번 챕터에서는 신경망과 순전파에 대해 정리 하였다.
신경망에서는 활성화 함수로 시그모이드 함수와 ReLU 함수 같은 매끄럽게 변화하는 함수를 이용한다.
기계 학습 문제는 크게 회귀와 분류로 나눌 수 있다.
출력층의 활성화 함수로는 회귀에서는 주로 항당 함수를, 분류에서는 주로 소프트맥스 함수를 이용한다.
입력 데이터를 묶은 것을 배치라고 하며 추론 처리를 이 배치 단위로 진행하면 결과를 훨씬 빠르게 얻을 수 있다.
