
기울기 소실 (Gradient Vanishing)
기울기 소실(Gradient Vanishing)이란 역전파(Backpropagation) 과정에서 입력층으로 갈수록 기울기(Gradient)가 점차적으로 작아지는 현상이다.
이는 신경망 구조에서 레이어가 늘어날 수록 악화되며 입력층에 가까운층들에서 가충치들이 제대로 업데이트 되지 않아 최적의 모델을 찾지 못하게 된다. 따라서 기울기 소실 문제는 신경망의 활성화 함수의 미분 결과 값(도함수 값)이 계속 곱해지면서 가중치에 따른 결과값의 기울기가 0이 되어 경사하강법(Gradient Descent)을 이용할 수 없게 된다.
기울기 폭주 (Gradient Exploding)
기울기 폭주는 기울기 소실과 반대되는 경우이다. 기울기가 점차 커져 가중치들이 비정상적으로 큰 값이 되어 발산되어 최적의 값을 찾지 못하는 현상이다.
기울기 소실 (Gradient Vanishing)과 폭주 (Exploding)를 완화하는 방법
1. 수렴하지 않는 활성화 함수 사용 - ReLU 함수와 LeakyReLU 함수
은닉층(hidden layer)의 활성화 함수로 시그모이드(sigmoid) 함수를 사용하면 역전파 과정에서 미분 연쇄 법칙(Chain rule) 시 시그모이드 함수는 0과 1 사이의 값을 출력하기 때문에 이 과정에서 미분 결과 값이 0으로 수렴하게 된다.


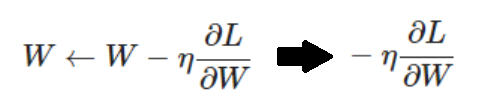
활성화 함수로 시그모이드 함수를 사용했을 때의 한계점을 개선하기 위해 제안된 tanh 함수는 0을 기준으로 출력 값이 -1 ~ 1 사이의 값을 갖는다.
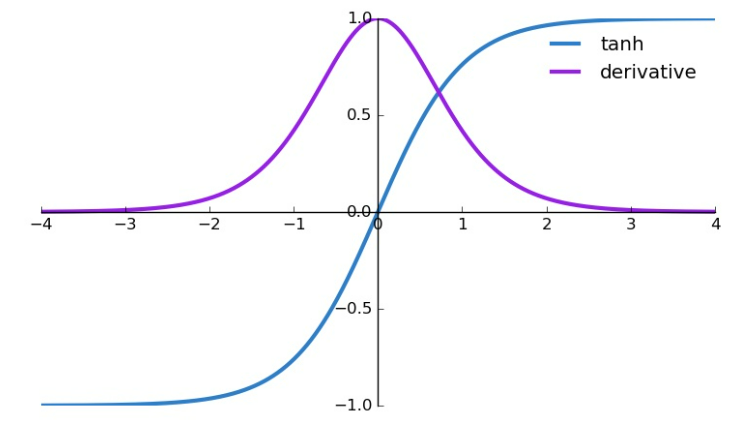
위 그림과 같이 미분값이 시그모이드 함수에 비해 커졌지만 tanh 함수 또한 x 값이 크거나 작아지면 기울기가 작아지기 때문에 기울기 소실 문제를 방지하는데 한계가 있다.
이러한 기울기 소실 문제를 해결하기 위해 활성화 함수로 ReLU(Rectified Linear Unit) 함수가 제안되었다.


ReLU 함수는 0보다 작은 값은 0으로 반환하며 0보다 큰 값은 값 그대로 반환하는 함수이다.
위 그림과 같이 입력 값에 상관없이 입력 값이 양수이면 항상 미분값은 1이기 때문에 역전파 과정에서 기울기가 소실되는 문제를 해결할 수 있다.
하지만 입력값이 음수일 땐 미분값이 항상 0이기 때문에 입력값이 음수인 경우에는 이후에 학습이 이루어지지 않는 한계가 있다. 이를 죽어가는 ReLU(Dying ReLU)라고 한다.
Dying ReLU 현상을 보완하기 위해 변형된 ReLU인 Leaky ReLU을 활성화 함수로 사용한다.

위 식에서 a는 하이퍼파라미터로 아주 작은 값을 나타낸다.
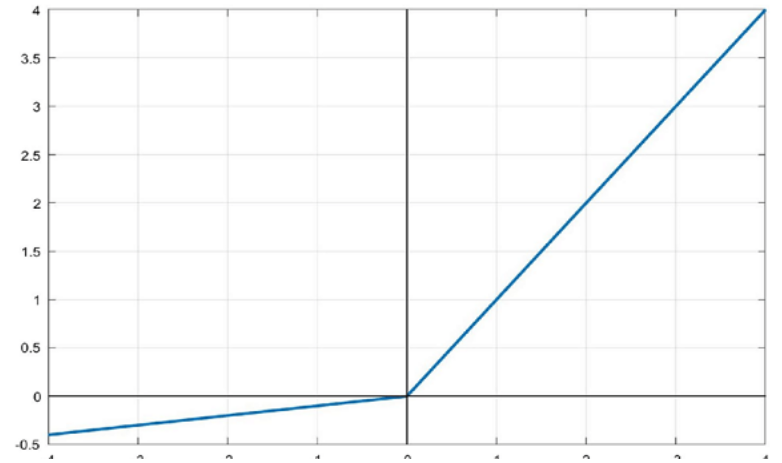
Leaky ReLU 함수는 입력값이 음수일 때 출력값을 0이 아닌 a가 곱해진 값을 출력하도록 하는 함수로 입력값이 음수여도 기울기가 0이 되지 않기 때문에 Dying ReLU 현상을 방지할 수 있다.
2. 그래디언트 클리핑 (Gradient Clipping)
그래디언트 클리핑은 기울기 폭주 문제를 완화하는 방법이다..
이는 역전파 과정에서 일정 임계값(threshold)을 넘지 못하게 기울기 값을 자르는 방법으로 임계값만큼 크기를 감소시켜 학습을 안정적으로 만든다.

그래디언트 클리핑을 하지 않게 되면 그래디언트가 급격하게 뛰어 global minimum에 도달하지 못하고 엉뚱한 방향으로 향하게 된다. 하지만 그래디언트 클리핑을 하게 되면 그래디언트 벡터가 방향을 유지하며 적은 값만큼만 이동하여 도달하고자 하는 곳으로 안정적으로 향하게 된다.
그래디언트 클리핑은 그래디언트의 L2 norm으로 나누는 방식으로 하게 된다. 임계값은 하이퍼파라미터로 그래디언트가 가질 수 있는 최대 L2 norm을 의미한다.

3. 배치 정규화 (Batch Normalization)
위의 두 방법을 사용하여도 기울기 소실과 폭주는 학습 중에 발생하기도 한다. 따라서 학습 과정 자체를 전체적으로 안정화하여 학습 속도를 가속시킬 수 있는 근본적인 방법인 배치 정규화를 사용하는 것이 좋다.
보통 정규화는 학습을 더 빨리 하기 위해서 사용하거나 Local optimum 문제에 빠질 가능성을 줄이기 위해 사용한다.

네트워크의 각 레이어나 Activation 마다 입력값의 분산이 달라지는 현상은 학습의 불안정화를 유발하므로 각 레이어의 입력의 분산을 평균 0, 표준편차 1인 입력값으로 정규화를 시켜 해결하는 Whitening의 한계점을 해결하도록 한 것이 배치 정규화이다.

배치 정규화는 미니 배치의 평균과 분산을 이용해 정규화 한 후 scale 및 shift를 감마 값, 베타 값을 통해 실행한다. 여기서 감마 값과 베타 값은 학습이 가능한 변수로 역전파를 통해 학습된다.
간단히 말해 배치 정규화는 한번에 들어오는 배치 단위로 입력에 대해 평균을 0으로 만들고 정규화를 하는 것이다.
배치 정규화는 각 층에서 활성화 함수를 통과하기 전이나 후에 모델을 하나 추가하여 입력값을 원점에 맞춰 정규화하여 정규화 된 데이터에 대해 두 개의 새로운 파라미터를 사용해 스케일과 시프트를 수행한다.
신경망의 첫번째 층으로 배치 정규화를 추가하면 배치 정규화 층이 훈련 세트를 표준화 해주는 역할을 하기 때문에 별도로 훈련 세트를 표준화 하지 않아도 된다.
배치 정규화를 사용하면 각 층의 입력값의 평균과 표준편차를 맞춰 가중치 초기화에 덜 민감해지며 학습 속도를 개선할 수 있고 기울기 소실 문제도 개선할 수 있다.
하지만 배치 정규화는 모델을 복잡하게 만들며 실행 시간을 느리게 만든다. 또, 너무 작은 배치 크기에서는 제대로 작동하지 않을 수 있다.
참고 링크 :
