
Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference, Benoit Jacob et al., 2017 을 읽고 요약, 정리한 내용입니다.
◼️ Abstract
모바일·엣지 기기에서 모델을 정수 연산만으로 추론하도록 만드는 8비트 양자화 스킴과, 그에 맞춘 양자화-인지 학습(시뮬레이티드/페이크 양자화) 절차를 제안한다.
정확도를 최대한 유지하면서도 지연 시간과 전력/메모리를 크게 줄이는 것이 목표이다.
MobileNet 계열에서도 정확도–지연시간 균형이 개선됨을 ImageNet/COCO에서 보여준다.
모든 연산을 float 대신 int8(+ 일부 int32 누적)로 바꿔도 정확도를 거의 잃지 않게, 학습부터 방법을 같이 설계한다.
◼️ Introduction
- 기존 경량화 흐름은 MobileNet/ShuffleNet 같은 효율적 아키텍처 설계와 양자화로 나뉘다.
- 기존 양자화 연구는 과대매개변수화된 네트워크(AlexNet/VGG 등) 기준이라 큰 압축률을 보이는 것은 당연하다.
- → 의미 있는 효율 개선을 보여주기 어려움, MobileNet 같은 모델을 양자화 하는 게 더 도전적이료 현실적.
- 가중치만 양자화 하는 방식 등은 저장 공간은 줄여도 연산 효율 증명은 부족하다.
- → 온디바이스 측정이 잘 제시되지 않는다.
- 1-bit/2-ary 네트워크처럼 곱셈을 비트연산으로 대체하는 방법은 특수 하드웨어에서는 유리하지만 일반 cpu에서는 이점이 제한적이다.
- → weight와 activation 모두 낮은 비트로 만들면 곱셈 자체 연산 cost가 높지 않다.
- 본 논문 기여:
- 정수-전용 quantization scheme : weight와 activation은 8-bit 정수, bias는 32-bit 정수로
- 정수-산술만으로 추론이 가능한 구현 : Qualcomm Hexagon 같은 정수 하드웨어에 효율적이며, ARM NEON 최적화 구현 제시
- 위 추론 경로에 맞춘 quantized training framework로 정확도 손실 최소화
- MobileNet 기반 분류, 검출에서 지연-정확도 트레이드오프가 실제 ARM CPU에서 눈에 띄게 개선됨을 벤치마크로 제시(ImageNet, COCO 등)
- x86에서의 고정소수점 가속, 저정밀 학습 가속 등의 선행을 참고하되, 본 연구는 모바일 CPU에서의 “추론” 속도–정확도 균형 개선에 집중한다.
- 아이디어
- “훈련은 float로 하되, 훈련 그래프 안에 ‘정수처럼 거칠게 보이게 하는 노드’(페이크 양자화)를 넣어 정수화 후 추론 환경을 미리 연습시킨다.
- 추론은 정수 연산만(int8 가중치·활성, int32 누적/바이어스)으로 돌게 통일한다.
- 이렇게 학습–추론을 함께 설계해 정확도 손실을 최소화 하는 것이다.
- 왜 정수만 쓰는지
- 모바일 cpu는 정수용 SIMD(MAC) 회로가 깔려 있기 때문에 여기에 맞추면 곱셈, 덧셈이 파이프라인으로 빠르게 돌아가게 된다.
- 반면 1-bit/bit shift 기반 방식은 특정 하드웨어에선 좋을 수 있으나 일반 cpu에 선 반드시 이득이 아니라 정확도 손실이 커질 수 있다.
- int8 전면 도입 + 정확도 방어가 현실적인 균형점이다.
- 왜 MobileNet이 benchmark인지
- 이미 작고 빠른 모델을 더 줄이거나 더 빠르게 만들 수 있음을 보여줘야 설득력 있기 때문이다.
- 정리
- 정수만으로 합성곱 레이어를 계산하고 바이어스는 int32로 더하고 activation(ReLU)은 정수 범위에서 클램프, 마지막에 재양자화로 int8로 출력하는 과정을 하나의 파이프라인으로 처리한다.
- 학습 시 그 효과를 흉내 내며 파라미터가 양자화 환경에 적응하도록 한다.
◼️ Quantized Inference
본 논문이 쓰는 양자화는 정수 q와 실수 r를 다음 affine 관계로 잇는다.
r=S(q−Z)
여기서 S는 스케일, Z는 제로 포인트(실수 0이 정수로 정확히 표현되도록 맞추는 오프셋)이다.
각 활성 텐서와 가중치 텐서는 자기만의 S, Z 한 쌍을 가짐. 일반적으로 가중치/활성은 8비트 정수, 일부는 32비트 정수로 양자화 한다. → 추론 시 모든 산술을 정수로만 구현할 수 있다.
제로 포인트는 “실수 0에 대응하는 정수값”이 되도록 잡는데, 이는 경계 패딩 등에서 “0을 정확히 표현”해야 하는 합성곱 구현에 유리하다.
구현 관점에서는 (예: TFLite) 양자화 텐서가 정수 배열 q, 스케일 S, 제로 포인트 Z를 함께 가진 구조로 관리되고 학습은 부동소수로 하되, 추론은 정수-전용으로 돌아가도록 설계한다.
⇒ 데이터를 “눈금 간격 S”과 “영점 Z”가 있는 눈금자로 측정한다고 생각하면 된다. 정수 q만 저장 해 두고 필요할 때 r=S(q-Z)로 실수값을 복원한다. 제로 포인트 덕분에 실수 0 → 정수 Z가 정확히 매핑되어 패딩/마스킹 처리가 깔끔해진다. 가중치, 활성은 int8, 바이어스는 누적 정밀도 때문에 int32로 둔다.
Integer-arithmetic-only matrix multiplication

실수 스케일 곱 M을 정수로 근사한 배율x오른쪽 시프트로 바꿔치기 한다.
int32 곱 → 반올림 시프트 만으로 실수 배율 효과를 재현하고 합은 계속 int32로 누적한다.
→ 부동소수 연산 없이 행렬곱/합성곱이 구현된다.
Efficient handling of zero-points



매 연산마다 (q-Z)를 뺄 필요 없이 한 번에 정리해 행/열 합만 미리 계산해 두고 코어는 unit8xuint8 → int32 누적에 집중한다.
⇒ 제로 포인트가 있어도 속도가 떨어지지 않는다.
Implementation of a typical fused layer
양자화된 행렬곱(또는 합성곱) 결과에 바이어스 더하기와 활성함수(예: ReLU/ReLU6 클램프), 그리고 재양자화(다운스케일+캐스트) 를 한 파이프라인으로 묶어(fuse) 처리한다.
→ 이렇게 해야 학습 그래프의 페이크 양자화 위치와 추론의 연산 단위가 일치하기 때문이다.
바이어스는 32비트 정수로 두고 스케일은 입력, 가중치 스케일의 곱(Sbias=S1S2)이고 제로 포인트는 0으로 둔다. 그 다음 결과를 정규화 배율 M으로 고정소수점 곱+반올림 시프트 해 출력 스케일로 내려주고 포화 캐스트(ex. uint8의 [0, 255]) 범위에 맞춘다.
→ ReLU 같은 클램프형 활성을 쓰면 정수 영역에서 바로 처리 가능하다.
- 추론 파이프라인 정리⇒ 한번에 묶으면 메모리 왕복이 줄어들고 학습에서 시뮬레이션 한 것과 동일한 산술을 보장할 수 있다.
- int8 입력 → int32 누적(곱·합) → int32 바이어스 더하기 → ReLU/ReLU6로 클램프 → (정규화 배율) 고정소수점 곱 + 반올림 시프트 → int8(또는 uint8)로 재양자화
◼️ Training with simulated quantization
보통은 부동소수점으로 학습을 끝낸 뒤에 가중치만 양자화(PTQ)하는데, 큰 모델에선 그럭저럭 통하지만 소형 모델에선 정확도 하락이 크다.
대표적인 실패 원인은
(1) 채널 간 가중치 범위 차이가 매우 클 때(같은 레이어는 하나의 해상도만 쓰므로 작은 범위 채널이 상대적으로 큰 오차를 가짐)
(2) 아웃라이어 가중치가 전체 양자화 정밀도를 갉아먹는 경우
이다.
이를 해결하기 위해 순전파에서 양자화 효과를 ‘흉내’ 내도록 학습 그래프에 가중치/활성 페이크 양자화 노드를 삽입한다.
역전파는 평소대로 float로 진행하고, 가중치, 바이어스도 float로 저장해 미세 업데이트가 가능하게 둔다. 다만 순전파 경로는 추론 엔진이 실제로 수행할 정수-전용 연산을 부동소수점으로 모사한다.
- 가중치 : 합성곱/FC에 곱해지기 전에 양자화(BN을 쓰면 ‘폴딩’ 후 가중치를 양자화)
- 활성값 : 실제 추론에서 활성함수 위치에 맞춰 그 지점에서 양자화(예: Conv+Bias → ReLU6 → 양자화).
- ResNet류에선 바이패스 연결의 합 이후 위치도 반영

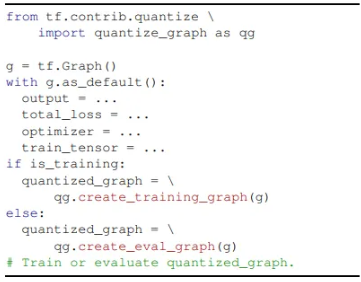
- float 모델의 트레이닝 그래프 생성 → 페이크 양자화 노드(가중치/활성 위치)에 삽입 → 시뮬레이티드 양자화 상태로 학습 수렴 → 인퍼런스 그래프 생성/최적화(퓨즈, 축소) → 정수-전용 인퍼런스로 실행
Learning quantization ranges
- 활성은 특히 데이터/학습 단계에 따라 값의 폭이 출렁이기 때문에, EMA로 서서히 추정해서 너무 이른 ‘과격한 제한’을 피하고자 한다.
- 0을 정확히 표현하도록 맞추는 건, §2의 제로 포인트 조건과 그대로 연결된다.
- 가중치, 활성의 “알맞은 눈금 눈치게임”
Batch normalization folding
BN을 쓰면, 학습 그래프에는 Conv → BN → ReLU처럼 분리돼 있지만, 추론 그래프에선 BN 파라미터를 가중치/바이어스에 흡수(fold) 해서 단일 Conv(+Bias) 로 만든다.
정확한 시뮬레이션을 위해 학습 중에도 폴딩된 등가 형태로 가중치를 양자화한다.

-> 바이어스 보정도 함께 이루어 짐
이렇게 폴딩하면 Fig 1.1a의 한번에 처리되는 fused layer와 동일한 구조로 학습, 추론이 맞춰진다.
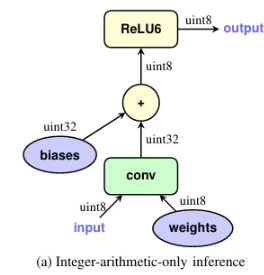
실제 폰/CPU에서는 Conv 한 번에 끝나는 경로가 빠르기 때문에 그래서 BN을 미리 가중치/바이어스에 흡수해 모양을 단순화하고, 그 단순화된 모양 그대로 양자화·학습·추론을 일치시킨다.
⇒ 이렇게 해야 학습 때 “흉내 낸 산술”과 배포 후 “진짜 산술”이 어긋나지 않게 된다.
◼️ Discussion
신경망의 부동소수점 계산을 정수 산술만으로 근사하는 양자화 스킴을 제안한다.
양자화 효과를 훈련 단계에서 시뮬레이션하면, 원래(부동소수) 모델과 거의 동일한 수준의 정확도를 회복할 수 있으며 또한 모델 크기를 4배 줄이는 것과 더불어, ARM NEON 기반 구현을 통해 추론 효율도 향상된다.
이 개선은 일반적인 ARM CPU에서의 지연 시간과 정확도 사이의 최신 균형(state-of-the-art)을 한 단계 끌어올리며 제안한 양자화 스킴과 효율적 아키텍처 설계의 시너지는, 정수-전용 추론이 실시간 및 저가형 휴대폰 시장에서 시각 인식 기술을 확장시키는 핵심 촉매가 될 수 있음을 시사한다.
